CMR đường thẳng (d) y=(3-2m )x - m^2 - 2m luôn tiếp xúc với một parabol cố định

Những câu hỏi liên quan
Tìm đường thẳng d cố định luôn tiếp xúc với đồ thị hàm số
(
C
)
:
y
x
2
-
(
2
m
+
3
)
x
+
m
2
+...
Đọc tiếp
Tìm đường thẳng d cố định luôn tiếp xúc với đồ thị hàm số ( C ) : y = x 2 - ( 2 m + 3 ) x + m 2 + 2 m (m là tham số thực)
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án D
kiểm tra hệ phương trình 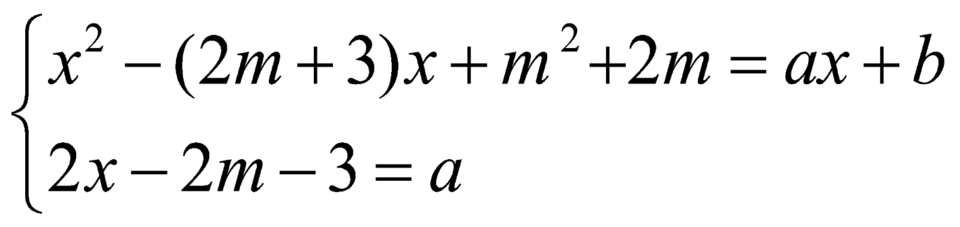 có nghiệm với mọi x, trong đó
có nghiệm với mọi x, trong đó ![]() là phương trình các đường thẳng có trong các phương án chọn.
là phương trình các đường thẳng có trong các phương án chọn.
Đúng 0
Bình luận (0)
Bài 10: Trong hệ toạ độ xOy cho Parabol (P) y = \(-\dfrac{x^2}{4}\) và đường thẳng (d): y= mx-2m-1
1. Vẽ (P)
2. Tìm m sao cho (P) và (d) tiếp xúc nhau.Tìm toạ độ tiếp điểm
3. Chứng tỏ rằng (d) luôn đi qua một điểm cố định
Cho Parabol : y=ax2 (P) và hàm số (d) : y=mx+2m+1
a,CMR (d) luôn đi qua điểm M cố định \(\forall m\)
b,Viết phương trình đường thẳng đi qua M và tiếp xúc với (P)
cá voi xanh không ? :))))
Cho đường thẳng d(m) : \(y=\left(\frac{m^2-1}{2m}\right)x+\frac{2m+1}{m}\) \(\left(m\ne0\right)\)
Chứng minh d(m) luôn tiếp xúc với một đường tròn cố định
cho đường thẳng (d): y=2mx+2m-3 và parabol (P): y=x^2 tìm m để đường thẳng tiếp xúc với parabol P
pt hoành độ giao điểm: \(x^2-2mx-2m+3=0\)
Để đường thẳng tiếp xúc với parabol thì pt có 1 nghiệm duy nhất
\(\Rightarrow\Delta'=0\)
\(\Delta'=m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1. Cho đường thẳng (d):y=2mx+2m-3 và Parabol (P):y=x\(^2\)
a) Tìm m để đường thẳng (d) đi qua A(1;5)
b) Tìm m để đường thẳng (d) tiếp xúc với Parabol (P)
a: Thay x=1 và y=5 vào (d), ta được:
2m+2m-3=5
=>4m-3=5
hay m=2
b: Phương trình hoành độ giao điểm là:
\(x^2-2mx-2m+3=0\)
Để(P) tiếp xúc với (d) thì \(\left(-2m\right)^2-4\left(-2m+3\right)=0\)
\(\Leftrightarrow4m^2+8m-12=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
=>m=-3 hoặc m=1
Đúng 1
Bình luận (0)
Tìm đường thẳng d cố định luôn tiếp xúc với đồ thị hàm số
C
:
y
x
2
-
2
m
+
3
x
+
m
2
+
2
m
(m là tham số thực). A. y x+1 B. y -x+1 C. y x-1 D. y -x-1
Đọc tiếp
Tìm đường thẳng d cố định luôn tiếp xúc với đồ thị hàm số C : y = x 2 - 2 m + 3 x + m 2 + 2 m (m là tham số thực).
A. y = x+1
B. y = -x+1
C. y = x-1
D. y = -x-1
Chọn D
Kiểm tra hệ phương trình
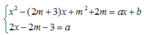
có nghiệm với mọi x, trong đó y=ax+b là phương trình các đường thẳng có trong các phương án chọn.
Đúng 0
Bình luận (0)
Chứng minh rằng họ đường thẳng sau luôn tiếp xúc với một đường cong cố định \(\left(C_m\right):y=2mx^3-x^2+\left(2m+1\right)x-m^2+2\)
Giả sử \(M\left(x_0;y_0\right)\) là điểm mà họ \(\Delta_{\alpha}\) không đi qua. Khi đó phương trình sau vô nghiệm với mọi m : \(m^2-2\left(x^3_0+x_0\right)m+y_0+x^2_0-x_0-2=0\)
\(\Leftrightarrow\Delta'=\left(x^3_0+x_0\right)^2-\left(y_0+x^2_0-x_0-2\right)< 0\)
\(\Leftrightarrow y_0>x^6_0+2x^4_0+x_0+2\)
Xét phương trình : \(2mx^3-x^2+\left(2m+1\right)x-m^2+2=x^6+2x^4+x+2\)
\(\Leftrightarrow m^2-2\left(x^3+x\right)m+\left(x^3+x\right)^2=0\)
\(\Leftrightarrow\left(x^3+x-m\right)^2=0\) (*)
Vì phương trình \(x^3+x-m=0\) luôn có nghiệm nên (*) luôn có nghiệm bội.
Vậy \(\left(C_m\right)\) luôn tiếp xúc với đường cong \(y=x^6+2x^4+x+2\)
Đúng 0
Bình luận (0)
CÁch 1: G/s họ đường thằng trên luôn tiếp xúc với parabol cố định: )
Khi đó: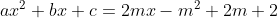 có nghiệm kép với mọi m
có nghiệm kép với mọi m
hay+c+m^2-2m-2=0) có nghiệm kép với mọi m
có nghiệm kép với mọi m
Cách 2: Gọi) là các điểm mà họ đường thẳng trên không đi qua.
là các điểm mà họ đường thẳng trên không đi qua.
Hay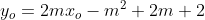 vô nghiệm ẩn m
vô nghiệm ẩn m
+y_o-2=0) vô nghiệm ẩn m
vô nghiệm ẩn m
^2-(y_o-2)%3C0&space;\\\Leftrightarrow&space;x_o^2+2x_o+3%3Cy_o)
Xét đường biên:y=x^2+2x+3)
Lập phương trình hoành độ giao điểm ta được:^2=0)
Phương trình này luôn có 1 nghiệm kép nên (dm) luôn tiếp xúc (P)
Khi đó:
hay
Cách 2: Gọi
Hay
Xét đường biên:
Lập phương trình hoành độ giao điểm ta được:
Phương trình này luôn có 1 nghiệm kép nên (dm) luôn tiếp xúc (P)
Đúng 0
Bình luận (0)
Cho đường thẳng (d): y= (m+1)x +2m -3. Chứng minh rằng với mọi m đường thẳng (d) luôn luôn đi qua một điểm cố định. Xác định điểm cố định đó.



















