thực hiện phép chia
2x^7+x^5+2 cho x^2+x+1
Những câu hỏi liên quan
thực hiện phép chia 2x^7+x^5+2 cho x^2+x+1
\(2x^7+x^5+2\div x^2+x+1=2x^5-3x^3-3x^2+1\left(dư1-x\right)\)
Đúng 0
Bình luận (0)
Thực hiện phép tính :Thực hiện phép tính :5.x^2(x-y+1)+(x^2-1)(x+y)6.(3x-5)(2x+11)-6(x+7)^2Bài 2: cho các đa thứcA (x+2) (x^2-2x+4)+2(x+1)(1-x); B (2x-y)^2 -2(4x^2-y^2)+(2x+y)^2+4(y+2)1/ Thu gọn đa thức A Và B.2/Tính giá trị của A tại x23/ Chứng minh rằng giá trị biểu thức B luôn dương với mọi giá trị của x,y
Đọc tiếp
Thực hiện phép tính :
Thực hiện phép tính :
5.x^2(x-y+1)+(x^2-1)(x+y)6.(3x-5)(2x+11)-6(x+7)^2
Bài 2: cho các đa thức
A= (x+2) (x^2-2x+4)+2(x+1)(1-x); B= (2x-y)^2 -2(4x^2-y^2)+(2x+y)^2+4(y+2)
1/ Thu gọn đa thức A Và B.
2/Tính giá trị của A tại x=2
3/ Chứng minh rằng giá trị biểu thức B luôn dương với mọi giá trị của x,y
Bài 2:
1: \(A=\left(x+2\right)\left(x^2-2x+4\right)+2\left(x+1\right)\left(1-x\right)\)
\(=\left(x+2\right)\left(x^2-x\cdot2+2^2\right)-2\left(x+1\right)\left(x-1\right)\)
\(=x^3+2^3-2\left(x^2-1\right)\)
\(=x^3+8-2x^2+2=x^3-2x^2+10\)
\(B=\left(2x-y\right)^2-2\left(4x^2-y^2\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y\right)^2-2\cdot\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y-2x-y\right)^2+4\left(y+2\right)\)
\(=\left(-2y\right)^2+4\left(y+2\right)\)
\(=4y^2+4y+8\)
2: Khi x=2 thì \(A=2^3-2\cdot2^2+10=8-8+10=10\)
3: \(B=4y^2+4y+8\)
\(=4y^2+4y+1+7\)
\(=\left(2y+1\right)^2+7>=7>0\forall y\)
=>B luôn dương với mọi y
Bài 1:
5: \(x^2\left(x-y+1\right)+\left(x^2-1\right)\left(x+y\right)\)
\(=x^3-x^2y+x^2+x^3+x^2y-x-y\)
\(=2x^3-x+x^2-y\)
6: \(\left(3x-5\right)\left(2x+11\right)-6\left(x+7\right)^2\)
\(=6x^2+33x-10x-55-6\left(x^2+14x+49\right)\)
\(=6x^2+23x-55-6x^2-84x-294\)
=-61x-349
Đúng 3
Bình luận (0)
Thực hiện phép tính sau:
a) (x+5)(x+1) - x^2
b) (x+4)2 - 6x + 7
thực hiện phép tính sau:
2 x ( 1/1 x 3 + 1/3 x 5 +1/5 x 7 +.......+ 1/13 x 15 )
\(=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{13\cdot15}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}=\dfrac{14}{15}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính :bài 1 :thực hiện phép tính :
Bài 3: phân tích thành nhân tử:3/6x(x-y)-9y^2+9xyBài 4:Tìm x, biết:
1/ (x-1)(x^2+x+1)-x^3-6x=11
2/ 16x^2-(3x-4)^2=0
3/ x^3-x^2+3-3x=0
4/ x-1/x+2=x+2/x+1
5/1/x+2/x+1=0
6/ 9-x^2/x : (x-3)=1
Xem chi tiết
Bài 3: phân tích thành nhân tử:3/6x(x-y)-9y^2+9xyBài 4:Tìm x, biết:
1/ (x-1)(x^2+x+1)-x^3-6x=11
2/ 16x^2-(3x-4)^2=0
3/ x^3-x^2+3-3x=0
4/ x-1/x+2=x+2/x+1
5/1/x+2/x+1=0
6/ 9-x^2/x : (x-3)=1
Bài 3:
3: \(6x\left(x-y\right)-9y^2+9xy\)
\(=6x\left(x-y\right)+9xy-9y^2\)
\(=6x\left(x-y\right)+9y\left(x-y\right)\)
\(=\left(x-y\right)\left(6x+9y\right)\)
\(=3\left(2x+3y\right)\left(x-y\right)\)
Bài 4:
Đúng 1
Bình luận (0)
Câu 1: Thực hiện phép tính
\(\dfrac{3}{7}x^2< 28x^5-7^3-\dfrac{14}{3}x^2-2\)
a, cho A dfrac{sqrt{x+1}}{sqrt{x-3}}. tìm x để A có giá trị nguyên ( x ϵ Z)b, Thực hiện phép tính: {[(2sqrt{2})^2 : 2,4] x [5,25 : (sqrt{7})^2]} : {[2dfrac{1}{7} : dfrac{left(sqrt{5}right)^2}{7}] : [2^2 : dfrac{left(2sqrt{2}right)^2}{sqrt{81}}]}
Đọc tiếp
a, cho A = \(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\). tìm x để A có giá trị nguyên ( x ϵ Z)
b, Thực hiện phép tính: {[(2\(\sqrt{2}\))\(^2\) : 2,4] x [5,25 : (\(\sqrt{7}\))\(^2\)]} : {[2\(\dfrac{1}{7}\) : \(\dfrac{\left(\sqrt{5}\right)^2}{7}\)] : [2\(^2\) : \(\dfrac{\left(2\sqrt{2}\right)^2}{\sqrt{81}}\)]}
a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
Đúng 0
Bình luận (0)
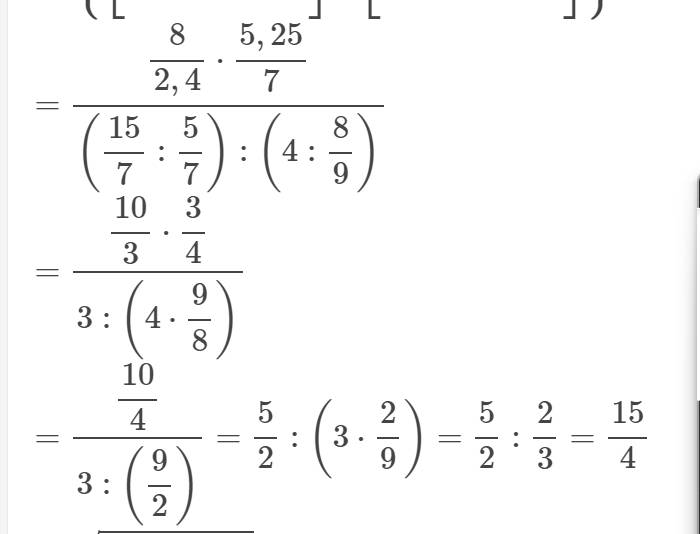
thực hiện phép tính
1)2x^2(-3x^2+2x-1)
2)(x-3)(x+7)-(x+5)(x-1)
3)-2x(-3x+2)-(x+2)^2
4)(2x-3)(x^2-2x-4)
1) \(-6x^4+4x^3-2x^2\)
2) \(=x^2+4x-21-x^2-4x+5=-16\)
3) \(=6x^2-4x-x^2-4x-4=5x^2-8x-4\)
4) \(=2x^3-4x^2-8x-3x^2+6x+12=2x^3-7x^2-2x+12\)
Đúng 0
Bình luận (0)
*Dạng 2: Đa thức BT1: Thực hiện phép tính a) 3x(x^2-5x+7) b) (x+4)(-x^2+6x+5) c) (3x-1)(3x+5)-7(x^2+2) d) (-5x^5 + 2x^4 - 1/3x^3): (-1/2x^3)
a: =3x^3-15x^2+21x
b: =-x^3+6x^2+5x-4x^2-24x-20
=-x^3+2x^2-19x-20
c: =9x^2+15x-3x-5-7x^2-14
=2x^2+12x-19
d: =10x^2-4x+2/3
Đúng 3
Bình luận (0)