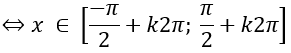Tìm tập xác định 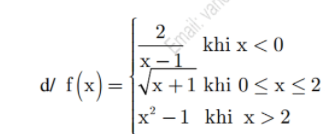

Những câu hỏi liên quan
Gọi tập xác định là D. Tìm tập xác định của hàm số
y
x
2
x
-
x
2
-
1
A.
D
R
/
0
,
1
B.
D...
Đọc tiếp
Gọi tập xác định là D. Tìm tập xác định của hàm số y = x 2 x - x 2 - 1
A. D = R / 0 , 1
B. D = R / 1
C. D = R / 0
D. D=(0,1)
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
tìm tập xác định \(y=tan15x\)
Để tìm tập xác định của hàm số y = tan(15x), ta cần xác định giá trị của x mà khi đưa vào hàm số, hàm số đó tồn tại và không gặp phải các giới hạn không xác định.
Trong trường hợp này, ta biết rằng hàm số tan(x) tồn tại và không xác định tại các điểm mà cos(x) = 0. Vì vậy, để tìm tập xác định của hàm số y = tan(15x), ta cần tìm tập xác định của 15x mà không gặp phải các giới hạn không xác định của hàm số tan(x).
Giới hạn không xác định của hàm số tan(x) xảy ra khi cos(x) = 0, tức x = (2n + 1)π/2, với n là số nguyên.
Áp dụng vào trường hợp của chúng ta, ta có:
15x = (2n + 1)π/2
Suy ra:
x = (2n + 1)π/30
Vậy, tập xác định của hàm số y = tan(15x) là tất cả các giá trị x thuộc tập:
x = (2n + 1)π/30, với n là số nguyên.
Đúng 0
Bình luận (0)
ĐKXĐ: 15x<>pi/2+kpi
=>x<>pi/30+kpi/15
TXĐ: D=R\{pi/30+kpi/15}
Đúng 0
Bình luận (0)
\(y=tan15x=\dfrac{sin15x}{cos15x}\\ ĐK:cos15x\ne0\\ \Rightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{30}+\dfrac{k2}{15}\\x\ne\dfrac{-\pi}{30}+\dfrac{k2}{15}\end{matrix}\right.\)
\(\Rightarrow TXĐ:R/\left(\dfrac{\pi}{30}+\dfrac{2k}{15};\dfrac{-\pi}{30}+\dfrac{2k}{15}\right)\)
Đúng 0
Bình luận (0)
Tìm tập xác định và tập giá trị của các hàm số sau:
Tìm tập xác định của hàm số
Đọc tiếp
Tìm tập xác định của hàm số ![]()
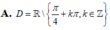
![]()
![]()
![]()
Tìm tập xác định của hàm số
ĐKXĐ:
a. \(x-1\ne0\Rightarrow x\ne1\)
b. \(sinx+1>0\Rightarrow sinx\ne-1\Rightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(cos\left(2x-\dfrac{\pi}{6}\right)\ne0\Rightarrow2x-\dfrac{\pi}{6}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{3}+\dfrac{k\pi}{2}\)
d. \(cos\left(3x-\pi\right)\ne0\Rightarrow cos3x\ne0\Rightarrow3x\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
e. \(sin^2x-cos^2x\ne0\Rightarrow cos2x\ne0\Rightarrow2x\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
g. \(cos2x-1\ne0\Rightarrow cos2x\ne1\Rightarrow2x\ne k2\pi\Rightarrow x\ne k\pi\)
Đúng 1
Bình luận (0)
Tìm tập xác định của hàm số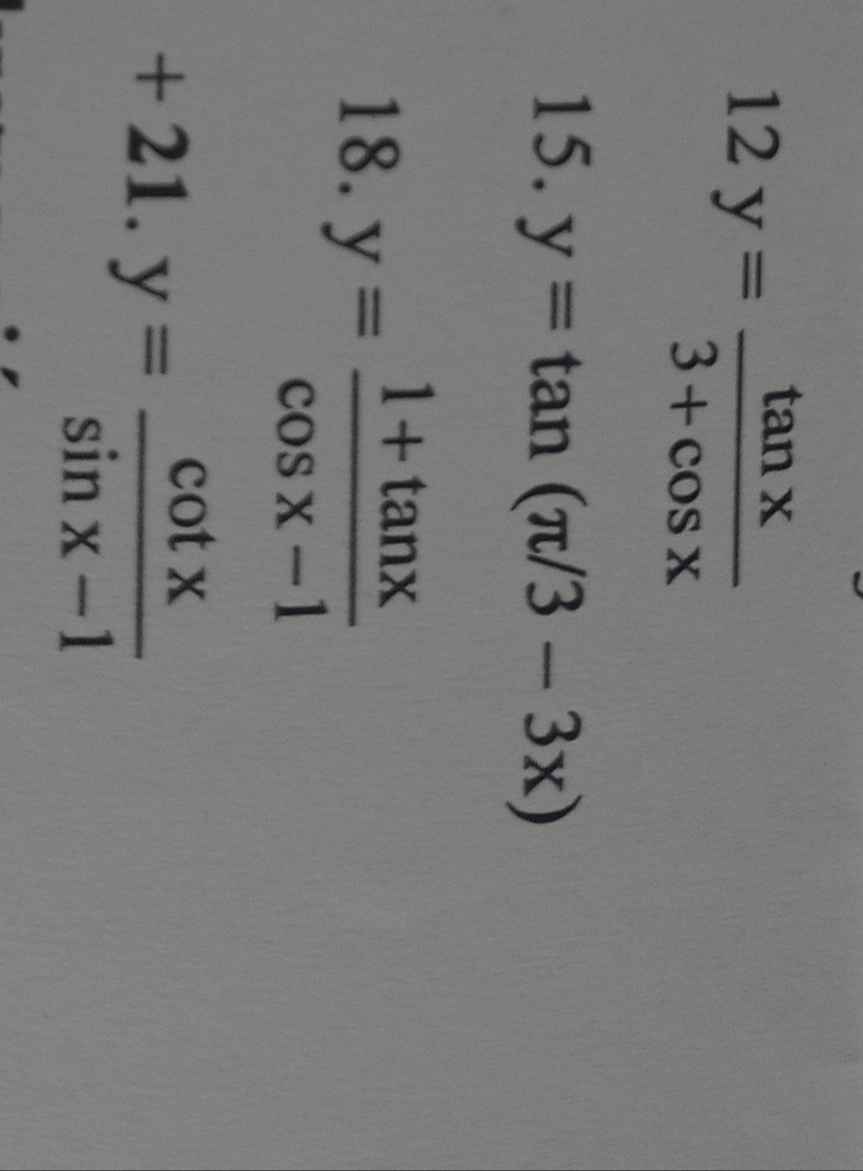
12.
Hàm số xác định khi: \(3+cosx\ne0\Leftrightarrow cosx\ne-3\Leftrightarrow x\in R\)
\(\Rightarrow D=R\)
15.
Hàm số xác định khi: \(cos\left(\dfrac{\pi}{3}-3x\right)\ne0\Leftrightarrow\dfrac{\pi}{3}-3x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne-\dfrac{\pi}{18}-\dfrac{k\pi}{3}\)
\(\Rightarrow D=R\backslash\left\{-\dfrac{\pi}{18}-\dfrac{k\pi}{3};k\in Z\right\}\)
18.
Hàm số xác định khi: \(cosx-1\ne0\Leftrightarrow cosx\ne1\Leftrightarrow x\ne k2\pi\)
\(\Rightarrow D=R\backslash\left\{k2\pi;k\in Z\right\}\)
21.
Hàm số xác định khi: \(sinx-1\ne0\Leftrightarrow sinx\ne1\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow D=R\backslash\left\{\dfrac{\pi}{2}+k2\pi;k\in Z\right\}\)
Đúng 0
Bình luận (0)