B2: cho tam giác ABC có đường trung tuyến BM, CN. Biết BM<CN. Chứng minh AB < AC

Những câu hỏi liên quan
Cho tam giác ABC có AB<AC. Biết BM và CN là hai đường trung tuyến của tam giác ABC. CMR: BM<CN
cho tam giác abc có hai đường trung tuyến bm và cn nếu bm=cn thì tam giác abc là tam giác gì
Do \(BM\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AM=CM\)
Và \(CN\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AN=BN\)
Mà \(BM=CN\left(gt\right)\)
Từ đó suy ra: \(AM=CM=AN=BN\)
Ta lại có: \(AM+CM=AC\)
Và \(AN+BN=AB\)
Nên: \(AM=CM=AN=BN\)
\(\Rightarrow AM+CM=AN+BN\)
\(\Rightarrow AC=AB\)
Vậy \(\Delta ABC\) có \(AC=AB\) là tam giác cân tại \(A\)
Đúng 0
Bình luận (2)
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G .Cho biết NBC < MBC .Chứng minh BM
Xem chi tiết
Sao vi phạm vậy bạn " Lê Đông Quân "
tnlvprvth học lớp cao
Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Biết BM = CN. Chứng minh A G ⊥ B C .
Cho tam giác ABC, có hai đường trung tuyến BM, CN. Chứng minh tam giác ANC = tam giác AMB. Chứng minh CN = BM
Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường trung tuyến BM, CN. Biết góc ABM= góc ACN. CM: BM=CN
cho tam giác abc có ab< ac. bm và cn là hai đường trung tuyến của tam giác abc. chứng minh rằng cn> bm
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.
Tham khảo:
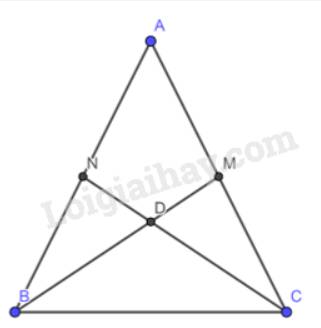
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
Đúng 0
Bình luận (0)
cho tam giác ABC, kẻ đường trung tuyến BM và CN. Biết BM nhỏ hơn CN. chứng minh AB nhỏ hơn AC





















