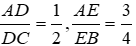Cho tam giác ABC có AB=AC=8cm; BC=6cm. Từddieemr M trên cạnh AB kẻ đường thẳng song song với BC cắt AC tại N. Xác định vị trí của M trên AB để BM=MN=NC. Tính độ dài BM.

Những câu hỏi liên quan
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết A. AC 4cm, BC 8cm, AB 6cmB. AB 4cm, BC 6cm, AC 8cmC. AB 4cm, BC 8cm, AC 6cmD. AB 8cm, BC 4cm, AC 6cm
Đọc tiếp
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết
A. AC = 4cm, BC = 8cm, AB = 6cm
B. AB = 4cm, BC = 6cm, AC = 8cm
C. AB = 4cm, BC = 8cm, AC = 6cm
D. AB = 8cm, BC = 4cm, AC = 6cm
TK
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án cần chọn là: C
Đúng 5
Bình luận (0)
Cho tam giác ABC có cạnh A B = 8 c m , B C = 8 c m , A C = 7 c m . So sánh các góc của tam giác ABC
A. ∠A > ∠B = ∠C
B. ∠A > ∠C > ∠B
C. ∠C > ∠B > ∠A
D. ∠C = ∠A > ∠B
Cho tam giác ABC có BC=10cm, AB=6cm và AC=8cm. Tam giác ABC là tam giác gì? vì sao?
Xét \(\Delta ABC:\)
\(BC^2=10^2=100.\\ AB^2+AC^2=6^2+8^2=100.\\ \Rightarrow BC^2=AB^2+AC^2.\)
\(\Rightarrow\Delta ABC\) vuông tại A (Pytago đảo).
Đúng 1
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh A B = 8 c m , A C = 8 c m , B C = 6 c m . Tìm góc nhỏ nhất của tam giác?
A. Góc A
B. Góc B
C. Góc C
D. Góc C và B
Do BC là cạnh nhỏ nhất nên góc C là góc nhỏ nhất. Chọn C
Đúng 0
Bình luận (0)
cho tam giác ABC có bc = 1cm ac=8cm cạnh AB là dộ dài số nguyên .tam giác ABC là tam giác ?
Áp dụng bất đẳng thức tam giác,ta có:
\(AC-BC< AB< AC+BC\)
\(8-1< AB< 8+1\)
\(7< AB< 9\)
mà cạnh AB là độ dài số nguyên
\(\Rightarrow\)\(AB=8cm\)
Do \(AB=AC\left(=8cm\right)\)
nên \(\Delta ABC\) cân tại A
Đúng 2
Bình luận (1)
cho tam giác ABC có AB=8cm, AC=12cn, góc A = 30 độ. Tính diện tích tam giác `ABC`.
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot8\cdot12\cdot sin30=24\left(cm^2\right)\)
Đúng 1
Bình luận (0)
\(S_{ABC}_{ }=\dfrac{1}{2}AB.AC.SinA=24dvdt\)
Đúng 1
Bình luận (0)
cho tam giác ABC là tam giác cân có AB=18cm; AC=8cm. Tính chu vi củ tam giác
Trường hợp 1: BC=18cm
=>NHận
=>C=AB+BC+AC=36+8=44(cm)
TRường hợp 2: BC=8cm
=>LOại
Đúng 0
Bình luận (0)
cho tam giác ABC có AB=8CM ; AC=6CM và BC=10CM . Chứng minh rằng tam giác ABC là tam giác vuông tại A
Ta có:
\(AB^2+AC^2=8^2+6^2=64+36=100\left(cm\right)\)
\(BC^2=10^2=100\left(cm\right)\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pi-ta-go đảo)
Đúng 2
Bình luận (0)
Áp dụng định lý Pytago đảo ta có:
AB2+AC2=82+62=100
mà 102=100
⇒82+62=102hay AB2+AC2=BC2
vậy ABC là tam giác vuông tại A
Đúng 1
Bình luận (0)
áp dụng định lý pitago ta có :
ab^2+ac^2=8^2+6^2=100=10^2
=>bc=10cm
=>tam giác abc vuông tại a
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
b. So sánh các góc của tam giác ABC
b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)
Đúng 0
Bình luận (0)
Cho tam giác ABC có các cạnh
A
B
6
c
m
,
B
C
8
c
m
,
A
C
7
c
m
.
So sánh các góc của tam giác ABC. A. ∠A ∠B ∠C B. ∠A ∠C ∠B C. ∠C ∠B ∠A D. ∠C ∠A ∠B
Đọc tiếp
Cho tam giác ABC có các cạnh A B = 6 c m , B C = 8 c m , A C = 7 c m . So sánh các góc của tam giác ABC.
A. ∠A > ∠B > ∠C
B. ∠A > ∠C > ∠B
C. ∠C > ∠B > ∠A
D. ∠C > ∠A > ∠B
Có AB < AC < BC ⇒ ∠C < ∠B < ∠A hay . ∠A > ∠B > ∠C . Chọn A
Đúng 0
Bình luận (0)