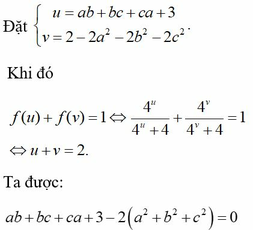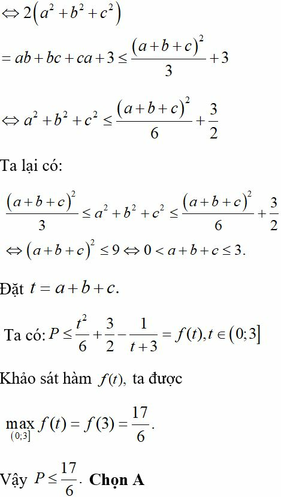Cho a+b+c=0.Chứng minh rằng N=1-(ab+2c2)(bc+2a2)(ca+2b2) là số dương

Những câu hỏi liên quan
cho a, b,c >0 thỏa mãn ab+bc+ca=abc
CMR : (√b2+2a2)/ab + (√c2+2b2)/bc + (√a2+2c2)/ac
Cho a+b+c=0 . CM các biểu thức sau không phụ thuộc vào biến số
A=((4bc-a2)/(bc+2a2))×((4ca-b2)/(ca+2b2))×((4ab-c2)/(ab+2c2))
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
cho 3 số thực dương không âm thỏa mãn a+b+c1
tìm MAX của P√a2+2b2+√b2+2c2+√c2+2a2
Đọc tiếp
cho 3 số thực dương không âm thỏa mãn a+b+c=1
tìm MAX của
Dấu "=" xảy ra khi và các hoán vị
Đúng 2
Bình luận (0)
Bài 1. Cho x, y là hai số nguyên dương thỏa mãn x2 + 2y là một số chính phương. Chứng minh rằng x2 + y là tổng của hai số chính phương
Bài 2. Cho a, b là hai số nguyên. Chứng minh rằng 2a2+2b2 là tổng của hai số chính phương
Bài 2:
Ta có: 2a2+2b2=(a2+2ab+b2)+(a2-2ab+b2)
=(a+b)2+(a-b)2 là tổng 2 số chính phương
⇒2a2+2b2 là tổng của 2 số chính phương(đpcm)
Đúng 0
Bình luận (0)
1.a)Cho các số dương a,b,c có tích bằng 1.Chứng minh rằng (a+1)(b+1)(c+1) lớn hơn hoặc bằng 8.
b)Chocacs số a và b không âm.Chứng minh rằng (a+b)(ab+1) lớn hơn hoặc bằng 4ab.
2.Cho các số dương a,b,c,d có tích bằng 1.Chứng minh rằng a bình +b bình +c bình +d bình +ab+cd lớn hơn hoặc bằng 6.
3.Chứng minh rằng nếu a+b+c>0.abc>0.ab+bc+ca>0 thì a>0,b>0,c>0.
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
Đúng 0
Bình luận (0)
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
Đúng 0
Bình luận (0)
sai rồi. sửa a+b=a+1, b+c=b+1, a+c=c+1 nha, thông cảm, nhìn sai đề
Đúng 0
Bình luận (0)
cho 3 số dương a, b, c thoả mãn ab+bc+ca=1. chứng minh rằng 1/ab + 1/bc + 1/ca >=3+ √(1/a²)+1 +√(1/b²)+1 +√(1/c²)+1
Biến đổi like that:
\(VT=\sum\dfrac{1}{ab}=\sum\dfrac{ab+bc+ca}{ab}=\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)+3\)
nên chỉ cần :\(\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\ge\sum\sqrt{\dfrac{1}{a^2}+1}=\sum\dfrac{\sqrt{a^2+1}}{a}\)
Áp dụng AM-GM:
\(\dfrac{\sqrt{a^2+1}}{a}=\dfrac{\sqrt{a^2+ab+bc+ca}}{a}=\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{a}\le\dfrac{2a+b+c}{2a}\)
Áp dụng tương tự:
\(VP=\sum\dfrac{\sqrt{a^2+1}}{a}\le\sum\dfrac{2a+b+c}{2a}=3+\dfrac{1}{2}\sum\left(\dfrac{b}{a}+\dfrac{c}{a}\right)\)
BĐT đúng khi ta chứng minh được
\(VT=\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\ge3+\dfrac{1}{2}\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\)
Điều này hiển nhiên đúng theo AM-GM:
\(\dfrac{1}{2}\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)=\dfrac{1}{2}\left(\dfrac{c}{a}+\dfrac{c}{b}+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{b}{c}\right)\ge\dfrac{1}{2}.6\sqrt[6]{\dfrac{a^2b^2c^2}{a^2b^2c^2}}=3\)
\(\Rightarrow\)đpcm
Dấu = xảy ra khi a=b=c
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực dương thỏa mãn a+b+c=1. Chứng minh rằng:
\(\frac{a+bc}{b+c}+\frac{b+ca}{c+a}+\frac{c+ab}{a+b}\ge\) 2
\(\frac{a+bc}{b+c}+\frac{b+ac}{c+a}+\frac{c+ab}{a+b}\)
\(=\frac{a\left(a+b+c\right)+bc}{b+c}+\frac{b\left(a+b+c\right)+ac}{a+c}+\frac{c\left(a+b+c\right)+ab}{a+b}\)
\(=\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}+\frac{\left(c+a\right)\left(c+b\right)}{a+b}\)
Áp dụng bđt Cô Si: \(\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(a+b\right)\)
Tương tự,cộng theo vế và rút gọn =>đpcm
Đúng 0
Bình luận (0)
\(\frac{a+bc}{b+c}+\frac{b+ac}{c+a}+\frac{c+ab}{a+b}\)
\(=\frac{a\left(a+b+c\right)+bc}{b+c}+\frac{b\left(a+b+c\right)+ac}{a+c}+\frac{c\left(a+b+c\right)+ab}{a+b}\)
\(=\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}+\frac{\left(c+a\right)\left(c+b\right)}{a+b}\)
Áp dụng bđt CÔ si
\(\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(a+b\right)\)
.............
Câu 1: Chứng minh frac{1}{1.2}+frac{1}{2.3}+frac{1}{3.4}+...+frac{1}{(n-1)n} với ∀n∈N^*Câu 2: Cho a,b,c là các số thực dương. Chứng minh rằng: frac{a^4+b^4+c^4}{a+b+c}geq abc.Câu 3: Cho các số thực dương a,b,c thỏa mãn ab+bc+ca3. Chứng minh rằng: sqrt{a^6+b^6+1}+sqrt{b^6+c^6+1}+sqrt{c^6+a^6+1}geq 3sqrt{3}Câu 4: Cho các số thực không âm a,b,c thỏa mãn a+b+c3.Chứng minh rằng: a^3+b^3+c^3geq 3Câu 5: Với a,b,c0 thỏa mãn điều kiện frac{a}{b}+frac{b}{c}+frac{c}{a}1. Chứng minh rằng: sqrtfrac{b}{a}+sqr...
Đọc tiếp
Câu 1: Chứng minh \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{(n-1)n}\) với ∀n∈\(N^*\)
Câu 2: Cho a,b,c là các số thực dương. Chứng minh rằng: \(\frac{a^4+b^4+c^4}{a+b+c}\geq abc\).
Câu 3: Cho các số thực dương a,b,c thỏa mãn \(ab+bc+ca=3\). Chứng minh rằng: \(\sqrt{a^6+b^6+1}+\sqrt{b^6+c^6+1}+\sqrt{c^6+a^6+1}\geq 3\sqrt{3}\)
Câu 4: Cho các số thực không âm a,b,c thỏa mãn \(a+b+c=3\).Chứng minh rằng: \(a^3+b^3+c^3\geq 3\)
Câu 5: Với \(a,b,c>0\) thỏa mãn điều kiện \(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\). Chứng minh rằng: \(\sqrt\frac{b}{a}+\sqrt\frac{c}{b}+\sqrt\frac{a}{c}\leq 1\)
1. Đề thiếu
2. BĐT cần chứng minh tương đương:
\(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Ta có:
\(a^4+b^4+c^4\ge\dfrac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{3}\left(ab+bc+ca\right)^2\ge\dfrac{1}{3}.3abc\left(a+b+c\right)\) (đpcm)
3.
Ta có:
\(\left(a^6+b^6+1\right)\left(1+1+1\right)\ge\left(a^3+b^3+1\right)^2\)
\(\Rightarrow VT\ge\dfrac{1}{\sqrt{3}}\left(a^3+b^3+1+b^3+c^3+1+c^3+a^3+1\right)\)
\(VT\ge\sqrt{3}+\dfrac{2}{\sqrt{3}}\left(a^3+b^3+c^3\right)\)
Lại có:
\(a^3+b^3+1\ge3ab\) ; \(b^3+c^3+1\ge3bc\) ; \(c^3+a^3+1\ge3ca\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow VT\ge\sqrt{3}+\dfrac{6}{\sqrt{3}}=3\sqrt{3}\)
Đúng 2
Bình luận (1)
4.
Ta có:
\(a^3+1+1\ge3a\) ; \(b^3+1+1\ge3b\) ; \(c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3\left(a+b+c\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
5.
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\) ; \(\dfrac{a}{b}+\dfrac{c}{a}\ge2\sqrt{\dfrac{c}{b}}\) ; \(\dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\)
\(\Rightarrow\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}+\sqrt{\dfrac{a}{c}}\le\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=1\)
Đúng 1
Bình luận (0)
Câu 1:
\(VT=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(VT=1-\dfrac{1}{n}< 1\) (đpcm)
Đúng 1
Bình luận (0)