Hai đường chéo AC và BD vuông góc với nhau tại I.

- Đường thẳng AB có hệ số góc bằng 2, do đó ta có

tgα = 2 ⇒ α = 63 ° 26 ' (tính trên máy tính bỏ túi).

Suy ra ∠ (ABD) ≈ 63 ° 26 '

Tam giác ABD cân, nên cũng có  ∠ (ADB) ≈  63 ° 26 '

Từ đó suy ra  ∠ (BAD) =  180 °  - 2.  63 ° 26 '  ≈  53 ° 8 '

Phương trình của đường thẳng AB có dạng: y = ax + b.

Do phương trình đi qua A(4;5) và B(1; -1) nên ta có:

5 = a.4 + b (1)

-1 = a.1 + b (2)

Trừ từng vế của (1) và (2), ta có: 6 = 3a ⇒ a = 2.

Thay a = 2 và (1) để tìm b, ta có 5 = 2.4 + b ⇒ b = -3.

Vậy phương trình đường thẳng AB là: y = 2x – 3.

Làm tương tự như trên, ta có:

Phương trình đường thẳng BC là: y = -x.

Phương trình đường thẳng CD là: y = x – 8.

Phương trình đường thẳng DA là: y = -2x + 13.

* Gọi phương trình đường thẳng AB là y = ax + b.

Tọa độ các điểm A, B phải thỏa mãn phương trình y = ax + b nên ta có:

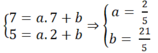
Vậy phương trình của đường thẳng AB là y = 2/5x + 21/5.

*Gọi phương trình của đường thẳng BC là y = a’x + b’.

Tương tự như trên ta có:

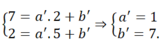
Vậy phương trình của đường thẳng BC là y = -x + 7.

*Gọi phương trình của đường thẳng AC là y = a’’x + b’’.

Tương tự như trên ta có: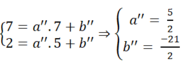 

Vậy phương trình của đường thẳng AC là y = 5/2x - 21/2.

Ta có

A B → = 1 ; 7 ⇒ A B = 1 2 + 7 2 = 5 2 B C → = − 7 ; 1 ⇒ B C = 5 2 C D → = − 1 ; − 7 ⇒ C D = 5 2 D A → = 7 ; − 1 ⇒ D A = 5 2 ⇒ A B = B C = C D = D A = 5 2 .

Lại có:  A B → . B C → = 1 − 7 + 7.1 = 0  nên A B ⊥ B C .

Từ đó suy ra ABCD là hình vuông.

Chọn C.

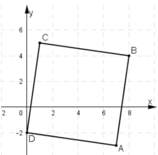
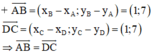
⇒ ABCD là hình bình hành.

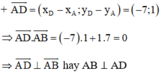
⇒ hình bình hành ABCD là hình chữ nhật.

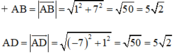
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).

a: Khi x=0 thì y=4

Khi y=0 thì -2x+4=0

hay x=2

b: Gọi điểm cần tìm là A(x;x)

Thay y=x vào y=-2x+4, ta được:

x=-2x+4

=>x=4

Vậy: Điểm cần tìm là A(4;4)

\(\overrightarrow{AB}=\left(-3;7\right)\)

\(\overrightarrow{DC}=\left(1-x_D;5-y_D\right)\)

Để ABCD là hbh thì 

\(\left\{{}\begin{matrix}1-x_D=-3\\5-y_D=7\end{matrix}\right.\Leftrightarrow D\left(2;-2\right)\)

* Áp dụng định lý Py-ta-go vào tam giác vuông lần lượt có các cạnh huyền là AB, AC, BC và sử dụng máy tính bỏ túi, tính được AB ≈ 5,39cm; AC ≈ 5,39; BC ≈ 4,24cm.

Do chu vi của tam giác ABC là AB + BC + CA ≈ 15,02cm

*Diện tích tam giác ABC bằng diện tích hình vuông cạnh dài 5cm trừ đi tổng diện tích ba tam giác vuông xung quanh (có cạnh huyền lần lượt là AB, BC, CA). Tính được: S A B C  = 10,5 ( c m 2 ).

Chọn C