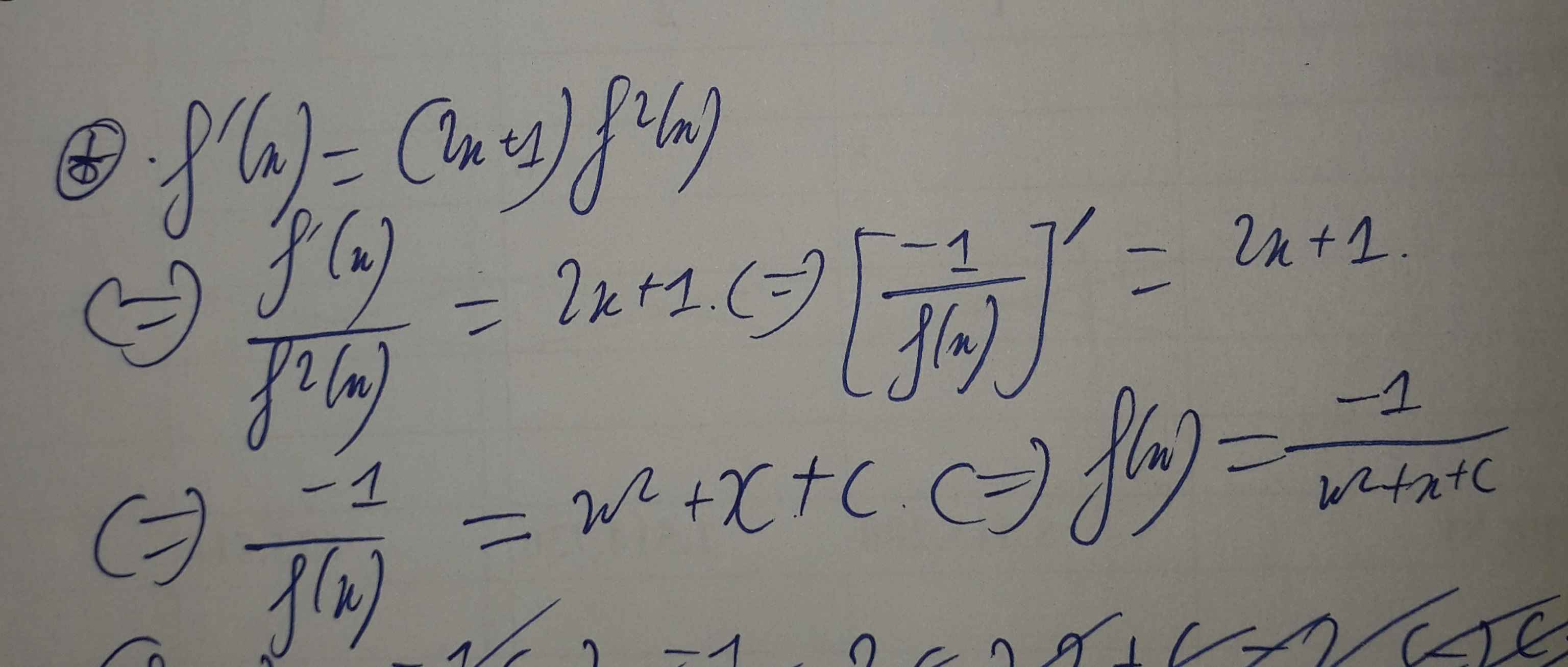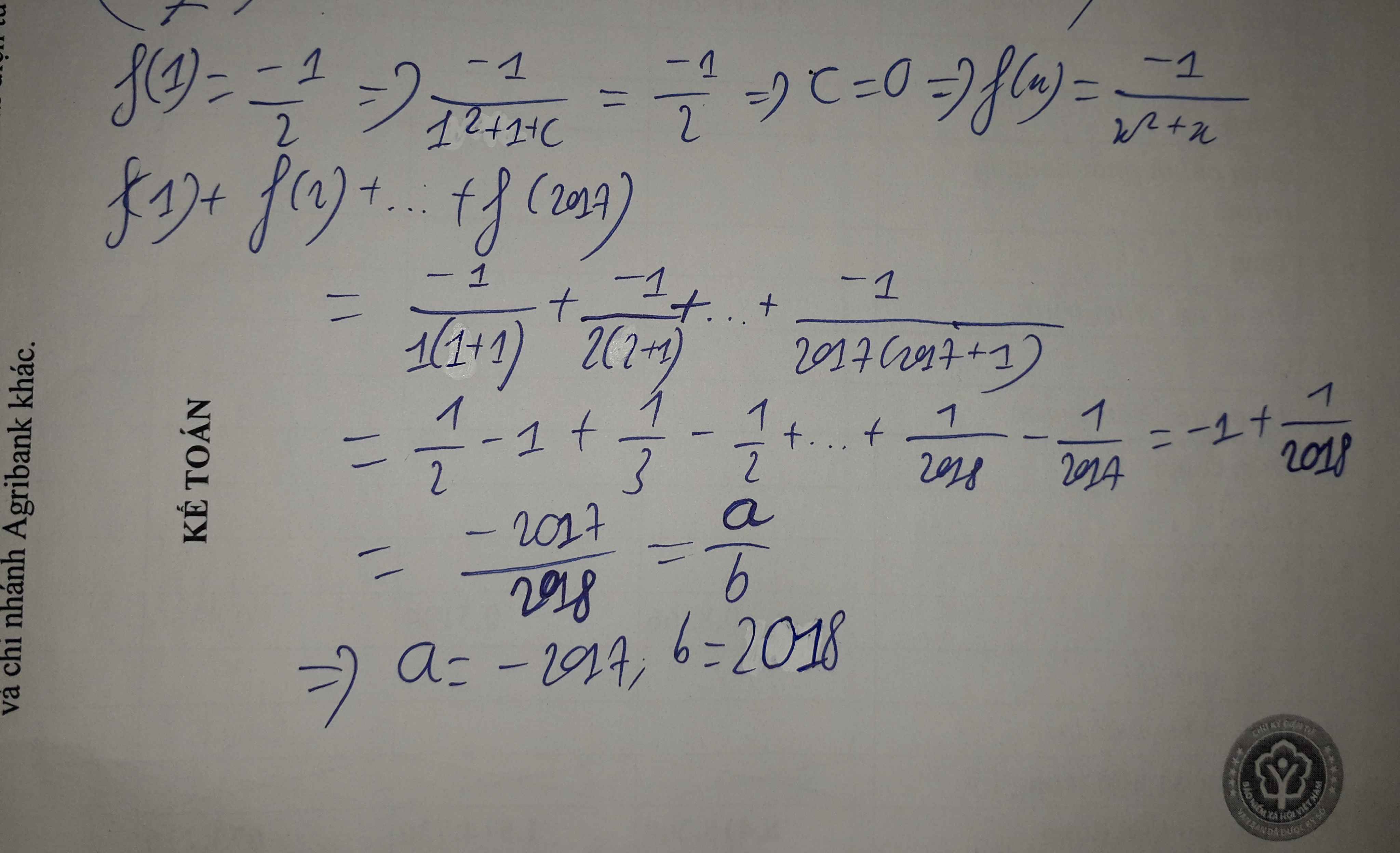Cho đa thức f(x) = \(a\left(x-2017\right)^2+\left(a\ne0;c\ne0\right)\). Hỏi nếu a và c là hai số cùng dấu thì đa thức f(x) có nghiệm không? Vì sao?

Những câu hỏi liên quan
1. Cho fleft(xright)x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1
gleft(xright)1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}
Tính giá trị của đa thức h(x) tại x2012, biết hleft(xright)left(fleft(xright)+gleft(xright)right).left(gleft(xright)-fleft(xright)right)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) ax + b với ane0, biết f(-1) 1 và f(1) -1
b) Tam thức bậc hai gleft(xright)ax^2+bx+c với ane0, biết g(-2) 9, g(-1) 2, g(1)6
3. a) Đa thức f(x) ax + b left(ane0right). Biết f(0) 0...
Đọc tiếp
1. Cho \(f\left(x\right)=x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1\)
\(g\left(x\right)=1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}\)
Tính giá trị của đa thức h(x) tại x=2012, biết \(h\left(x\right)=\left(f\left(x\right)+g\left(x\right)\right).\left(g\left(x\right)-f\left(x\right)\right)\)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) = ax + b với \(a\ne0\), biết f(-1) = 1 và f(1) = -1
b) Tam thức bậc hai \(g\left(x\right)=ax^2+bx+c\) với \(a\ne0\), biết g(-2) = 9, g(-1) = 2, g(1)=6
3. a) Đa thức f(x) = ax + b \(\left(a\ne0\right)\). Biết f(0) = 0. Chứng minh f(x) = -f(-x) với mọi x
b) Đa thức f(x) = ax2 + bx + c \(\left(a\ne0\right)\). Biết f(1) = f(-1). Chứng minh f(x) = f(-x) với mọi x.
Cho đa thức \(f\left(x\right)=ax^2+bx+c\) \(\left(a\ne0\right)\). Tìm a, b, c biết \(f\left(x\right)-2020\)chia hết cho x - 1, \(f\left(x\right)+2021\) chia hết cho x + 1 và \(f\left(x\right)\) nhận giá trị bằng 2 khi x = 0
Mình có nghĩ ra cách này mọi người xem giúp mình với
f(x) = \(ax^2+bx+c\)
Ta có f(0) = 2 => c = 2
Ta đặt Q(x) = \(ax^2+bx+c-2020\)
và G(x) = \(ax^2+bx+c+2021\)
f(x) - 2020 chia cho x - 1 hay Q(x) chia cho x - 1 được số dư
\(R_1\) = Q(1) = \(a.1^2+b.1+c-2020=a+b+c-2020\)
Mà Q(x) chia hết cho x-1 nên \(R_1\) = 0
hay \(a+b+c-2020=0\). Mà c = 2 => a + b = 2018 (1)
G(x) chia cho x + 1 số dư
\(R_2\) = G(-1) = \(a.\left(-1\right)^2+b.\left(-1\right)+c+2021=a-b+2+2021\)
Mà G(x) chia hết cho x + 1 nên \(R_2\)=0
hay \(a-b+2+2021=0\) => \(a-b=-2023\) (2)
Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(f\left(0\right)=2\Rightarrow c=2\)
\(f\left(x\right)-2020\) chia hết \(x-1\Rightarrow f\left(1\right)-2020=0\)
\(\Rightarrow a+b+c-2020=0\Rightarrow a+b-2018=0\)
\(f\left(x\right)+2021\) chia hết \(x+1\Rightarrow f\left(-1\right)+2021=0\)
\(\Rightarrow a-b+c+2021=0\Rightarrow a-b+2023=0\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b
1. Cho đa thức Pleft(xright)ax^2+bx+cleft(ane0right). CMR tồn tại nhiều nhất một đa thức Qleft(xright) bậc n thỏa mãn Pleft(Qleft(xright)right)Qleft(Pleft(xright)right)
2. Cho a,b,c là các số dương thỏa a^2+b^2+c^2+abc4. CMR a+b+cge asqrt{bc}+bsqrt{ca}+csqrt{ab}
Giúp mình làm mấy bài này với, vài ngày nữa mình phải nộp rồi mà đến giờ mình vẫn chưa nghĩ ra được ý tưởng gì cả. Mình cảm ơn trước nhé.
Đọc tiếp
1. Cho đa thức \(P\left(x\right)=ax^2+bx+c\left(a\ne0\right)\). CMR tồn tại nhiều nhất một đa thức \(Q\left(x\right)\) bậc \(n\) thỏa mãn \(P\left(Q\left(x\right)\right)=Q\left(P\left(x\right)\right)\)
2. Cho \(a,b,c\) là các số dương thỏa \(a^2+b^2+c^2+abc=4\). CMR \(a+b+c\ge a\sqrt{bc}+b\sqrt{ca}+c\sqrt{ab}\)
Giúp mình làm mấy bài này với, vài ngày nữa mình phải nộp rồi mà đến giờ mình vẫn chưa nghĩ ra được ý tưởng gì cả. Mình cảm ơn trước nhé.
Cho a,b,c là các số thực và \(a\ne0\). Chứng minh rằng nếu đa thức \(f\left(x\right)=a\left(ax^2+bx+c\right)^2+b\left(ax^2+bx+c\right)+c\) vô nghiệm thì phương trình \(g\left(x\right)=ax^2+bx-c\) có hai nghiệm trái dấu
Với \(c=0\Rightarrow f\left(x\right)=0\) có nghiệm \(x=0\) (loại)
TH1: \(a;c\) trái dấu
Xét pt \(f\left(x\right)=0\Leftrightarrow a\left(ax^2+bx+c\right)^2+b\left(ax^2+bx+c\right)+c=0\)
Đặt \(ax^2+bx+c=t\) \(\Rightarrow at^2+bt+c=0\) (1)
Do a; c trái dấu \(\Leftrightarrow\) (1) luôn có 2 nghiệm trái dấu.
Không mất tính tổng quát, giả sử \(t_1< 0< t_2\)
\(\Rightarrow\left[{}\begin{matrix}ax^2+bx+c=t_1\\ax^2+bx+c=t_2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}ax^2+bx+c-t_1=0\left(2\right)\\ax^2+bx+c-t_2=0\left(3\right)\end{matrix}\right.\)
Mà a; c trái dấu nên:
- Nếu \(a>0\Rightarrow c< 0\Rightarrow c-t_2< 0\Rightarrow a\left(c-t_2\right)< 0\)
\(\Rightarrow\) (3) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)
- Nếu \(a< 0\Rightarrow c>0\Rightarrow c-t_1>0\Rightarrow a\left(c-t_1\right)< 0\)
\(\Rightarrow\left(2\right)\) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)
Vậy đa thức \(f\left(x\right)\) luôn có nghiệm khi a; c trái dấu
\(\Rightarrow\)Để \(f\left(x\right)=0\) vô nghiệm thì điều kiện cần là \(a;c\) cùng dấu \(\Leftrightarrow ac>0\)
Khi đó xét \(g\left(x\right)=0\) có \(a.\left(-c\right)< 0\Rightarrow g\left(x\right)=0\) luôn có 2 nghiệm trái dấu (đpcm)
Đúng 0
Bình luận (0)
Cho đa thức hệ số nguyên fleft(xright)thỏa mãn:fleft(m^2+n^2right)f^2left(mright)+f^2left(nright),forall m,nnguyên dương và fleft(xright)nhận giá trị dương với xne0. Biết fleft(0right)0, fleft(1right)ne0. Tính fleft(3right)
Đọc tiếp
Cho đa thức hệ số nguyên \(f\left(x\right)\)thỏa mãn:
\(f\left(m^2+n^2\right)=f^2\left(m\right)+f^2\left(n\right),\forall m,n\)nguyên dương và \(f\left(x\right)\)nhận giá trị dương với \(x\ne0\). Biết \(f\left(0\right)=0\), \(f\left(1\right)\ne0\). Tính \(f\left(3\right)\)
Cho \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\) Hãy tính giá trị của biểu thức sau: \(A=f\left(\dfrac{1}{2017}\right)+f\left(\dfrac{2}{2017}\right)+...+f\left(\dfrac{2015}{2017}\right)+f\left(\dfrac{2016}{2017}\right)\)
Lời giải:
Ta thấy: \(f(x)=\frac{x^3}{1-3x+3x^2}\Rightarrow f(1-x)=\frac{(1-x)^3}{1-3(1-x)+3(1-x)^2}=\frac{(1-x)^3}{3x^2-3x+1}\)
\(\Rightarrow f(x)+f(1-x)=\frac{x^3}{1-3x+3x^2}+\frac{(1-x)^3}{3x^2-3x+1}=\frac{x^3+(1-x)^3}{3x^2-3x+1}=1\)
Do đó:
\(f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)=1\)
\(f\left(\frac{2}{2017}\right)+f\left(\frac{2015}{2017}\right)=1\)
............
\(f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)=1\)
Cộng theo vế:
\(\Rightarrow A=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+f\left(\frac{3}{2017}\right)+...f\left(\frac{2015}{2017}\right)+f\left(\frac{2016}{2017}\right)\)
\(=\underbrace{1+1+1...+1}_{1008}=1008\)
Đúng 0
Bình luận (0)
cho tam thức \(f\left(x\right)=ax^2+bx+c\left(a\ne0\right)\), \(\Delta=b^2-4ac\). ta có f(x)>0 với mọi x thuộc r khi và chỉ khi nào
f(x)>0 với mọi x khi và chỉ khi: \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b^2-4ac< 0\\a>0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Số dư khi chia đa thức \(f\left(x\right)=x^{2017}+2017x^2+2017x+1\) cho đa thức \(g\left(x\right)=x-1\) là
dam cong tian Làm giúp đi mk bó tay cái dạng này !! -_-
Đúng 0
Bình luận (2)
Xem thêm câu trả lời