-log²₂ x^2_  log₂x²- 20=0

↔ pt này vô ng bạn ơi!!! xem lại đầu bài.

Bài này phương trình có tận 4 nghiệm chứ không phải vô nghiệm đâu bạn Đỗ đại học nhé

Điều kiện \(x\ne0\)

Ta có từ phương trình ban đầu cho \(\Leftrightarrow4\log_2^2\left|x\right|-2\log_2\left|x\right|-20=0\)

                                                     \(\Leftrightarrow2\log_2^2\left|x\right|-\log_2\left|x\right|-10=0\)

Đặt \(t=\log_2\left|x\right|\) ta được phương trình \(2t^2-t-10=0\Leftrightarrow\begin{cases}t=-2\\t=\frac{5}{2}\end{cases}\)

Với \(t=2\Rightarrow\log_2\left|x\right|=-2\Leftrightarrow\left|x\right|=\frac{1}{4}\Leftrightarrow x=\pm\frac{1}{4}\)

Với \(t=\frac{5}{2}\Rightarrow\log_2\left|x\right|=\frac{5}{2}\Leftrightarrow\left|x\right|=\sqrt{32}\Leftrightarrow x=\pm\sqrt{32}\)

Vậy phương trình có 4 nghiệm : \(x=\frac{1}{4};x=-\frac{1}{4};x=\sqrt{32};x=-\sqrt{32}\)

a: ĐKXĐ: \(x\notin\left\{\dfrac{5}{2}\right\}\)

\(\log_32x-5=3\)

=>\(log_3\left(2x-5\right)=log_327\)

=>2x-5=27

=>2x=32

=>x=16(nhận)

b: ĐKXĐ: x<>0

\(\log_4x^2=2\)

=>\(log_4x^2=log_416\)

=>\(x^2=16\)

=>\(\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)

c: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{5}{2}\right\}\)

\(\log_7\left(3x-1\right)=\log_7\left(2x+5\right)\)

=>3x-1=2x+5

=>x=6(nhận)

d: ĐKXĐ: \(x\notin\left\{1;-1;\dfrac{-1+\sqrt{13}}{4};\dfrac{-1-\sqrt{13}}{4}\right\}\)

\(ln\left(4x^2+2x-3\right)=ln\left(3x^2-3\right)\)

=>\(4x^2+2x-3=3x^2-3\)

=>\(x^2+2x=0\)

=>x(x+2)=0

=>\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)

e: ĐKXĐ: \(x\notin\left\{-\dfrac{3}{2};\dfrac{1}{3}\right\}\)

\(log\left(2x+3\right)=log\left(1-3x\right)\)

=>2x+3=1-3x

=>5x=-2

=>\(x=-\dfrac{2}{5}\left(nhận\right)\)

a) Đặt t = 13^x > 0 ta được phương trình:

13t² – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0

⇔ t = 1 ⇔ 13^x = 1 ⇔ x = 0

b)

Chia cả hai vế phương trình cho 9^x ta được phương trình tương đương

Đặt (t > 0) , ta được phương trình:

(1 + t)(1 + 3t) = 8t ⇔ 3t² – 4t + 1 = 0 ⇔

Với ta được nghiệm

Với t = 1 ta được nghiệm x = 0

c) Điều kiện: x > 2

Vì nên phương trình đã cho tương đương với:

d) Điều kiện: x > 0

log₂²x – 5log₂x + 6 = 0

⇔(log₂x – 2)(log₂x – 3) = 0

⇔ x ∈ {4, 8}

a) 

ĐK: \(\left\{{}\begin{matrix}2x-4>0\\x-1>0\end{matrix}\right.\Leftrightarrow x>1\)

\(\log_5\left(2x-4\right)+\log_{\dfrac{1}{5}}\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(2x-4\right)-\log_5\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(\dfrac{2x-4}{x-1}\right)=\log_51\\ \Leftrightarrow\dfrac{2x-4}{x-1}=1\\ \Leftrightarrow2x-4=x-1\\ \Leftrightarrow x=3\left(tm\right)\)

Vậy x = 3.

b) ĐK: x > 0

\(\log_2x+\log_4x=3\\ \Leftrightarrow\log_2x+\dfrac{1}{2}\log_2x=3\\ \Leftrightarrow\left(1+\dfrac{1}{2}\right)\log_2x=3\\ \Leftrightarrow\dfrac{3}{2}\log_2x=3\\ \Leftrightarrow\log_2x=2\\ \Leftrightarrow x=4\left(tm\right)\)

Vậy x= 4

\(a,0,1^{2-x}>0,1^{4+2x}\\ \Leftrightarrow2-x>2x+4\\ \Leftrightarrow3x< -2\\ \Leftrightarrow x< -\dfrac{2}{3}\)

\(b,2\cdot5^{2x+1}\le3\\ \Leftrightarrow5^{2x+1}\le\dfrac{3}{2}\\ \Leftrightarrow2x+1\le log_5\left(\dfrac{3}{2}\right)\\ \Leftrightarrow2x\le log_5\left(\dfrac{3}{2}\right)-1\\ \Leftrightarrow x\le\dfrac{1}{2}log_5\left(\dfrac{3}{2}\right)-\dfrac{1}{2}\\ \Leftrightarrow x\le log_5\left(\dfrac{\sqrt{30}}{10}\right)\)

c, ĐK: \(x>-7\)

\(log_3\left(x+7\right)\ge-1\\ \Leftrightarrow x+7\ge\dfrac{1}{3}\\ \Leftrightarrow x\ge-\dfrac{20}{3}\)

Kết hợp với ĐKXĐ, ta có:\(x\ge-\dfrac{20}{3}\)

d, ĐK: \(x>\dfrac{1}{2}\)

\(log_{0,5}\left(x+7\right)\ge log_{0,5}\left(2x-1\right)\\ \Leftrightarrow x+7\le2x-1\\ \Leftrightarrow x\ge8\)

Kết hợp với ĐKXĐ, ta được: \(x\ge8\)

Chọn C

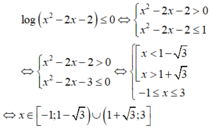
⇒  [ - 1 ;   1   -   3 )   ∪   ( 1   +   3 ;   3 ]

⇒ [ - 1 ;   1   -   3 )   ∪   ( 1   +   3 ;   3 ]

Chọn C