Cho tứ giác MNPQ có 2 đường chéo cắt nhau tại E và có cạnh MN=MQ;NP=PQ.Chứng minh a)MP là đường phân giác của góc M và P b) MP vuông góc với NQ Mn giúp em với Em cảm ơn ạ❤️

Những câu hỏi liên quan
Cho tứ giác MNPQ nội tiếp đường tròn đường kính MQ. Hai đường chéo MP và NQ cắt nhau tại E. Gọi F là điểm thuộc đường thẳng MQ sao cho EF vuông góc với MQ. Đường thẳng PF cắt đường tròn đường kính MQ tại điểm thứ 2 là K. Gọi L là giao điểm của NQ và PF. Chứng minh rằng: NQ.LE = NE.LQ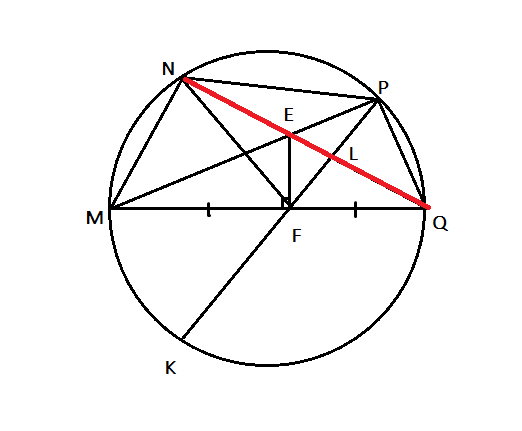
Cho tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại O. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh tứ giác MNPQ có các cạnh bằng nhau.
b) MP cắt AC và BD tại E và F. Chứng minh rằng tam giác OEF cân
a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MN//QP và MN=QP
Xét tứ giác MNPQ có
MN//QP(cmt)
MN=QP(cmt)
Do đó: MNPQ là hình bình hành
Xét ΔABD có
Q là trung điểm của AD
M là trung điểm của AB
Do đó: QM là đường trung bình của ΔABD
Suy ra: QM//DB và \(QM=\dfrac{DB}{2}\)
hay \(QM=\dfrac{AC}{2}\)(3)
Từ (2) và (3) suy ra QM=QP
Hình bình hành MNPQ có QM=QP(cmt)
nên MNPQ là hình thoi
Đúng 0
Bình luận (0)
Cho tứ giác MNPQ nội tiếp (O) đường kính MQ, hai đường chéo MF và NQ cắt nhau tại E .Gọi F là điểm thuộc MQ sao cho EF vuông góc với MQ .Đường thẳng PF cắt (O) tại điểm thứ 2 là K. OQ và PF cắt nhau tại L . cmr :
a, tứ giác QEFP nội tiếp
b, FM là tia phân giác của góc NFK
c, EN.QL=QL.EL
Cho Hình Chữ NHật MNPQ. Hai đường chéo MP và NQ cắt nhau tại O . Trên đoạn ON lấy điểm E . Lấy điểm F sao cho E là trung điểm của đoạn PF .
a) Cho MN =6 cm; MP =10 cm . Tính diện tích hcn MNPQ
b) c/m tứ giác MFNQ là hình thang
c)Gọi I, K là chân đường vuông góc kẻ từ F đến đoạn thẳng MQ , MN . C/m ba điểm I,K,E tẳng hàng
Cho hình chữ nhật MNPQ có độ dài các cạnh MN = 15cm , NP = 12 cm . Hai điểm E , F thuộc cạnh MN sao cho ME = NF = 6cm . Hai đường QF và PE cắt nhau tại K . Tính tỉ số KF / KQ và diện tích tứ giác MEKO ?
nè , em đăng bài nhầm đó à , thứ nhất :em lm đề sai / thứ 2 : em đăng muộn qá , ko ai còn on nữa ồi
Đúng 0
Bình luận (0)
c) 22/5 + 51/9 + 11/4 + 3/5 + 1/3 + 1/4
= 22/5 +3/5 +51/9 + 1/3 +11/4+1/4
= (22/5 +3/5) +(51/9 + 3/9) +(11/4+1/4)
= 25/5 +54/9 +12/4
= 5 +6 +3
= 14
d) (1/6 + 1/10 + 1/15) : (1/6 + 1/10 - 1/15)
= (5/30 + 3/30 +2/30 ) :(5/30 +3/30 -2/30)
= 10/30 : 6/30
= 1/3 : 1/5
= 5/3
Đúng 0
Bình luận (0)
Bạn vào trang này nha: https://th-so1taygiang-binhdinh.violet.vn/present/bai-toan-hinh-hoc-o-tieu-hoc-5750593.html
Đúng 0
Bình luận (0)
Cho tứ giác MNPQ nội tiếp (O) đường kính MQ . Hai đường chéo NF và NQ cắt nhau tại E . Gọi F là điểm thuộc EF vuống góc với NQ . Đường thẳng PF caw3ts (O) tại điểm thứ 2 là K . OQ và PE cắt nhau tại L . CNM RẰNG :
a)TỨ GIÁC QEFP NỘI TIẾP
B)FM LÀ TIA PG CỦA NFK
C)EN.QL=QN.EL
GIÚP MK VỚI MÌNH TÍCH CHO ! MÌNH CẦN GẤP TRƯỚC TỐI NAY . CẢM ƠN CÁC BẠN
Hình dễ tự vẽ
a ) + b )Ta có \(\widehat{MPQ}=90^o\)( góc nội tiếp chắn nửa đường tròn ) ; \(EF\perp MQ\Rightarrow\widehat{EPQ}+\widehat{EFQ}=90^o+90^o=180^o\)=> tứ giác PEFQ nội tiếp đường tròn đường kính PQ
Tương tự => \(\widehat{ENM}+\widehat{EFM}=90^o+90^o=180^o\)=> tứ giácMNEF nội tiếp => \(\widehat{PFQ}=\widehat{PEQ}\)( hai góc nội tiếp cùng chắn cung PQ trong đường tròn đường kính EQ )
\(\widehat{NFM}=\widehat{NEM}\)( hai góc nội tiếp cùng chắn cung MN trong đường tròn đường kính ME )
\(\widehat{NEM}=\widehat{PEQ}\)( hai góc đối đỉnh ) , \(\widehat{PFQ}=\widehat{MFK}\)( hai góc đối đỉnh )
\(\Rightarrow\widehat{NFM}=\widehat{KFM}\)hay FM là tia phân giác của \(\widehat{NFK}\)
c) Có : \(\widehat{NPM}=\widehat{NQM}\)( hai góc nội tiếp cùng chắn cung MN trong đường tròn đường kính MQ )
\(\widehat{EPF}=\widehat{EQF}\)( hai góc nội tiếp cùng chắn cung EF trong đường tròn đường kính EQ )
\(\Rightarrow\widehat{NPE}=\widehat{EPL}\) => PE là phân giác trong của \(\Delta NPL\). Lại có \(PE\perp PQ\)=> PE là phân giác ngoài của \(\Delta NPL\Rightarrow\frac{EN}{EL}=\frac{QN}{QL}\Rightarrow EN.QL=QN.EL\)(đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tứ giác MNPQ có NP=MQ và NP không song song với MQ. Gọi A,B,C,D,E,F lần lượt là trung điểm của các đoạn thẳng MN,NP,PQ,QM,MP.NP
a, chứng minh tứ giác AFCE là hình thoi
b, chứng minh AC,BD,EF cùng cắt nhau tại trung điểm
cho hình thang cân MNPQ có đáy nhỏ MN và hai đường chéo cắt nhau tại B và hai cạnh bên cắt nhau tại A
a) chứng minh tam giác AMN cân
b) chứng minh AB là trung trực của MN và PQ
a) Ta có: góc Q =góc P
=> AQ = AP ( quan hệ giữa góc và cạnh đối diện)
Ta có: AM + MQ = AQ
AN + NP = AP
Mà MQ = NP ( MNPQ là hình thang cân).
AQ = AP (cmt)
=> AM = AN => tam giác MAN cân tại A.
Câu b bạn tự làm nha
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AD = BC và AB < CD. Trung điểm của các cạnh AB và CD là M và N. Trung điểm của các đường chéo BD và AC là P và Q.
a) chứng minh tứ giác MNPQ là hình thoi
b) hai cạnh DA và CD kéo dài cắt nhau tại G. kẻ tia phân giác Gx của góc AGB. Chứng minh Gx //MN



















