Bài 1 :

a) M là trung điểm của đoạn thẳng AB 

\(\Rightarrow MA=MB=\frac{1}{2}AB\). Thật vậy : Do M là trung điểm của AB nên theo đĩnh nghĩa ta có  

:\(MA+MB=AB\)VÀ \(MA=MB\)

\(\Rightarrow2MA=2MB=AB\)

\(\Rightarrow MA=MB\frac{1}{2}AB\)

b) Nếu \(MA=MB=\frac{1}{2}AB\Rightarrow\)M là trung điểm của đoạn thằng AB

Từ \(MA=MB=\frac{1}{2}AB\Rightarrow MA+MB=\frac{1}{2}AB+\frac{1}{2}AB=AB\)

Vậy \(MA+MB=AB\)VÀ \(MA=MB\)

Chứng tỏ M là trung điểm đoạn thẳng AB

Bài 2 :

Gọi O là trung điểm chung của AB VÀ CD. Ta có:

Gỉa sử :A và C cùng phía đối với O 

Ta thấy rằng 

\(\hept{\begin{cases}AC=OC-OA\\BD=OD-OB\end{cases}}\)

\(\Leftrightarrow\)\(AC=BD\)

\(\hept{\begin{cases}AD=OA+OD\\BC=OB+OC\end{cases}}\)

\(\Leftrightarrow AD=BC\)

Trường hợp A,C khác phía đối với O chứng minh tương tự

Mk k vẽ được hình xin lỗi bạn nhiều nha!

Chúc bạn học tốt ( -_- )

Vì D là trung điểm của MA

\(\Rightarrow AD\text{=}DM\)hay DM=\(\frac{1}{2}AM\)

Tương tự: EM=EB hay EM=\(\frac{1}{2}MB\)

Ta có: DE=DM+ME=\(\frac{1}{2}AM\text{+}\frac{1}{2}MB\)=\(\frac{1}{2}\left(AM\text{+}MB\right)\text{=}\frac{1}{2}AB\)

Vậy DE có độ dài không đổi

D.MA+MB=AB và MA=MB

D.MA+MB=AB và MA=MB

D bạn nhé 

M là trung điểm của đoạn thẳng AB khi:
+ Điểm M nằm giữa hai điểm A và B
+ MA = MB =   
Vậy ta chọn đáp án đúng là: MA = MB = 

D

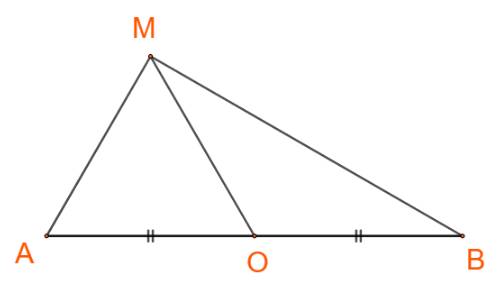
Ta có: \(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow 0  \Leftrightarrow  - \overrightarrow {OA}  = \overrightarrow {OB} \)

\(\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO}  + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO}  - \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO}  + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO}  + \overrightarrow {OB} } \right) = \overrightarrow {MA} .\overrightarrow {MB} \) (đpcm)