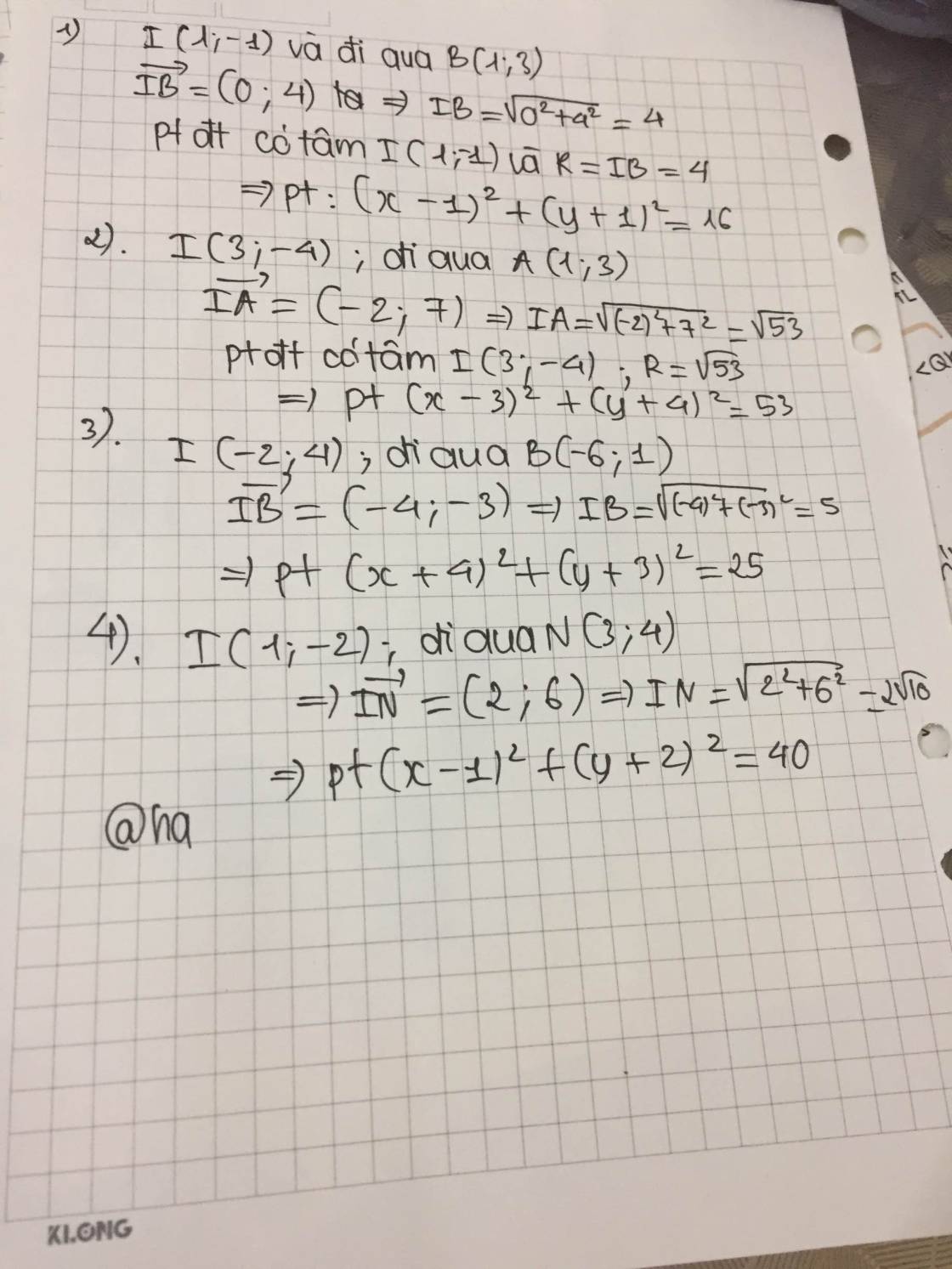(T) là đường tròn đi qua điểm A (3; 3), B (1; 1), C(5; 1). Dây cung MN vuông góc với bán kính của (T) tại điểm (3; 0). Tính độ dài đoạn thẳng MN

Những câu hỏi liên quan
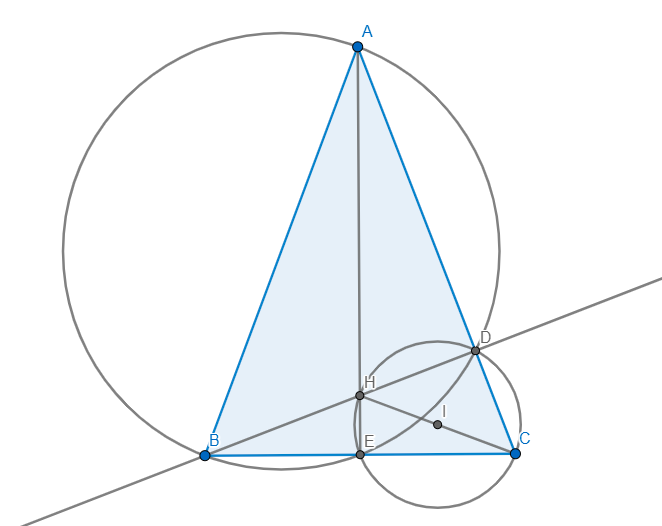
Cho tam giác ABC cân tại A, BD là đường cao, E là trung điểm của BC, H là giao điểm của
AE và BD.
a) Chứng minh 4 điểm A, D, E, B cùng thuộc đường tròn tâm O.
b) Xác định tâm I của đường tròn đi qua 3 điểm H, D, C.
c) Chỉ ra 2 điểm chung của đường tròn tâm (O) và đường tròn (I).
a) Vì tam giác ABC cân tại A có E là trung điểm BC
\(\Rightarrow AE\bot BC\Rightarrow\angle AEB=90\)
\(\Rightarrow\angle AEB=\angle ADB=90\Rightarrow ADEB\) nội tiếp
b) Vì \(\angle HDC=90\Rightarrow\left(HDC\right)\) là đường tròn đường kính HC
\(\Rightarrow\) tâm I của (HDC) là trung điểm HC
c) Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HDCE\) nội tiếp
\(\Rightarrow\left(I\right)\) đi qua điểm E và D
Vì ADEB nội tiếp \(\Rightarrow\left(O\right)\) đi qua điểm E và D
\(\Rightarrow\) 2 điểm chung là D và E
Đúng 2
Bình luận (0)
1) Viết pt đường tròn tâm l (1,-1) và đi qua điểm B (1,3) 2) Viết pt đường tròn tâm l (3,-4) và đi qua điểm A (1,3) 3) Viết pt đường tròn tâm l ( -2,4) , đi qua điểm B (-6,1) 4) viết pt đường tròn tâm l (1,-2) và đi qua điểm N ( 3,4) Giúp vs bạn
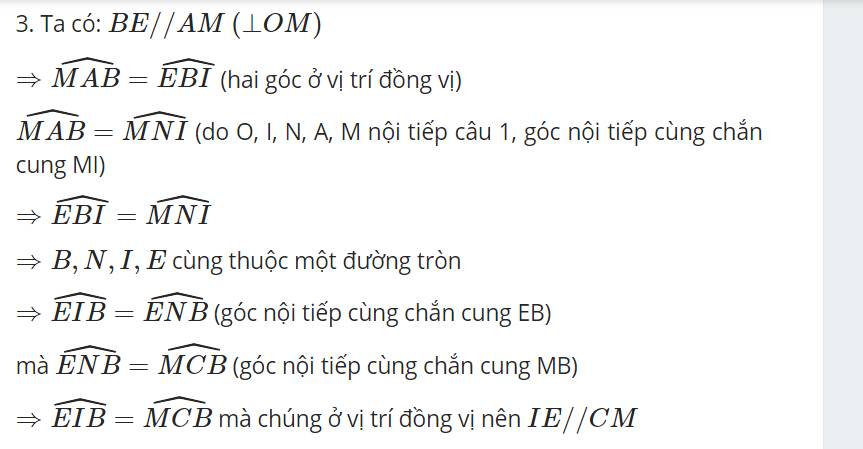
Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Qua A kẻ hai tiếng tuyến AM và AN tới đường tròn (M,N là hai tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O;R) tại B và C (AB<AC). Gọi I là trung điểm của BC.
Đường thẳng đi qua B, song song với AM, cắt MN tại E. CMR: IE song song MC
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (ABAC, đường thẳng d không đi qua tâm O)a) Chứng minh tứ giác AMON là tứ giác nội tiếpb) Chứng minh AN^2AB.ACc) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiệ...
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN\(^2\)=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (ABAC, đường thẳng d không đi qua tâm O)a) Chứng minh tứ giác AMON là tứ giác nội tiếpb) Chứng minh AN22AB.ACc) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiệ...
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
Giúp mình với đang cần gấp lắm!!
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
Đúng 0
Bình luận (0)
1/ Nếu cát tuyến MAB và tiếp tuyến MT của đường tròn (O;R) ,T là tiếp điểm thì MT2=MA.MB
2/Cho hai đường thẳng x,y cắt nhau tại M.Hai điểm A,B thuộc x,điểm T thuộc y sao cho MT2=MA.MB thì MT là tiếp tuyến của đường tròn đi qua ba điểm T,A,B(T là tiếp điểm)
Cho 3 điểm ABC theo thứ tự thằng hàng. Một đường tròn O đi qua hai điểm B và C. Từ điểm chính giữa M của cung nỏ BC đường kính MN cắt dây BC tại D. T a n cắt đường tròn tại điểm thứ hai I . Các dây BC,MI cắt nhau tại KA ) chứng minh rằng khi đường tròn Tâm O thay đổi nhưng vẫn đi qua hai điểm b và c thì đường MI luôn đi qua điểm cố địnhB) xác định đường tròn tâm O để đoạn thẳng MN có độ dài nhỏ nhất
Đọc tiếp
Cho 3 điểm ABC theo thứ tự thằng hàng. Một đường tròn O đi qua hai điểm B và C. Từ điểm chính giữa M của cung nỏ BC đường kính MN cắt dây BC tại D. T a n cắt đường tròn tại điểm thứ hai I . Các dây BC,MI cắt nhau tại K
A ) chứng minh rằng khi đường tròn Tâm O thay đổi nhưng vẫn đi qua hai điểm b và c thì đường MI luôn đi qua điểm cố định
B) xác định đường tròn tâm O để đoạn thẳng MN có độ dài nhỏ nhất
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.a.Chứng minh tứ giác AMNC nội tiếpb.Chứng minh DE vuông góc với MB
Đọc tiếp
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.
a.Chứng minh tứ giác AMNC nội tiếp
b.Chứng minh DE vuông góc với MB
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
Đúng 0
Bình luận (0)
Cho đường tròn (O) với dây AB. Gọi M là điểm chính giữa cung. C là 1 điểm thuộc đường kính AB ( C khác A, B). Tia MC cắt (O) tại D
a) CMR: MC. MD= MA²
b) Khi C di động thì tổng bán kính các đường tròn (O1) đi qua 3 điểm B, C, D và đường tròn (O2) đi qua 3 điểm A, C, D không đổi