Bài 4:Cho hình thang ABCD có góc A= góc D= 90 độ, AB= AD= 2cm; DC= 4cm và BH vuông góc CD tại H
a)Chứng minh rằng: tam giác ABD= tam giác HDB
b)Chứng minh rằng: tam giác BHC vuông cân tại H
hình thang vuông ABCD có góc A bằng góc D và bằng 90 độ, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang
Cho hình thang vuông ABCD, góc A= góc D=90 độ, AB=AD=2cm, BC=4cm
a,Tính các góc của hình thang
hình thang vuông ABCD có góc A bằng góc D và bằng 90 độ, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang
giup minh vs
diện tích hình thang = (đáy lớn + đáy bé)chiều cao : 2 = (2+4)x2:2= 6 cm^2
Lấy K là trung điểm của CD , I là trung điểm của DN
Chứng minh tứ giác ABKD là hình vuông
=> ˆADB=45o(1)ADB^=45o(1)
Chứng minh △ DBC△ DBC là tam giác vuông cân =>ˆDBC=90o(2)=>DBC^=90o(2)
Từ (1) và (2) ta được ˆABC=135oABC^=135o
Ta có △ DBN△ DBN vuông tại B có BI là trung tuyến nên BI =DI =IN (3)
lại có △ DMN△ DMN vuông tại M có MI là trung tuyến nên MI= DI =IN(4)
Kết hợp (3)(4) ta có +△ MIB+△ MIB cân tại I nên ˆIMB=ˆIBMIMB^=IBM^(5)
+△ OIN+△ OINcân tại I nên ˆIBN=ˆBNI(6)IBN^=BNI^(6)
Từ (5) (6) ta được : ˆIBM+ˆIBN+ˆIMB+ˆBNI=270oIBM^+IBN^+IMB^+BNI^=270o
=>ˆMIN=360o−270o=90o=>MIN^=360o−270o=90o
=>MI⊥ DN=>MI⊥ DN
Tam giác vuông DMN có MI vừa là tt vừa là đường cao nên là tam giác vuông cân
Cho hình thang vuông ABCD , góc A = góc D = 90 độ ; AB = 2cm ; CD = 4 cm ; góc C = 45 độ . Tính diện tích ABCD
Cho hình thang vuông ABCD , góc A = góc D = 90 độ ; AB = 2cm ; CD = 4 cm ; góc C = 45 độ . Tính diện tích ABCD
Cho hình thang vuông ABCD có A ^ = D ^ = 90 ° , AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 137 °
B. 136 °
C. 36 °
D. 135 °
Đáp án cần chọn là: D
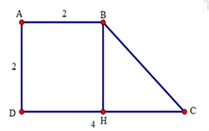
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .
Cho hình thang vuông ABCD có góc A = góc D = 90 độ và đường chéo BD vuông với cạch BC. Biết AB= 2cm, AD= 4cm. Tính chu vi và diện tích của hình thang vuông
Xét tam giác ABD và tam giác BDC có:
\(\widehat{BAD}=\widehat{DBC}=90^o\)
\(\widehat{ABD}=\widehat{BDC}\) (Cùng phụ với góc \(\widehat{ADC}\) )
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow BD^2=\frac{AB}{DC}\)
Xét tam giác vuông ABD, áp dụng định lý Pi-ta-go ta có:
\(DB^2=AB^2+AD^2=2^2+4^2=20\)
Suy ra \(2=\frac{20}{DC}\Rightarrow DC=10cm\)
Xét tam giác vuông BDC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=DC^2-BD^2=10^2-20=80\Rightarrow BC=\sqrt{80}\left(cm\right)\)
Vậy chu vi hình thang vuông bằng: 2 + 4 + 10 + \(\sqrt{80}=14+\sqrt{80}\left(cm\right)\)
Diện tích hình thang bằng: \(\frac{\left(2+10\right).4}{2}=24\left(cm^2\right)\)
Bài 1: Hình thang ABCD (AB//CD) có AB=AD+BC. Chứng minh rằng các tia phân giác của các góc C và D gặp nhau tại 1 điểm thuộc đáy AB
Bài 2: Hình thang vuông ABCD (góc A = góc D= 90°)có AB =4cm, CD=9cm, BC=13cm. Tính AD
Bài 3: hình thang vuông ABCD (góc A=góc D=90°)có AB =9cm,CD=15cm, AC=17cm. Tính độ dài cạnh bên
Cho hình thang ABCD, góc A = góc D = 90o, AB = AD = 2cm, CD = 4cm. Tính các góc của hình thang
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠ A = ∠ D = 90 0 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ∆ BHC vuông cân tại H
Hình đây ạ !!:
