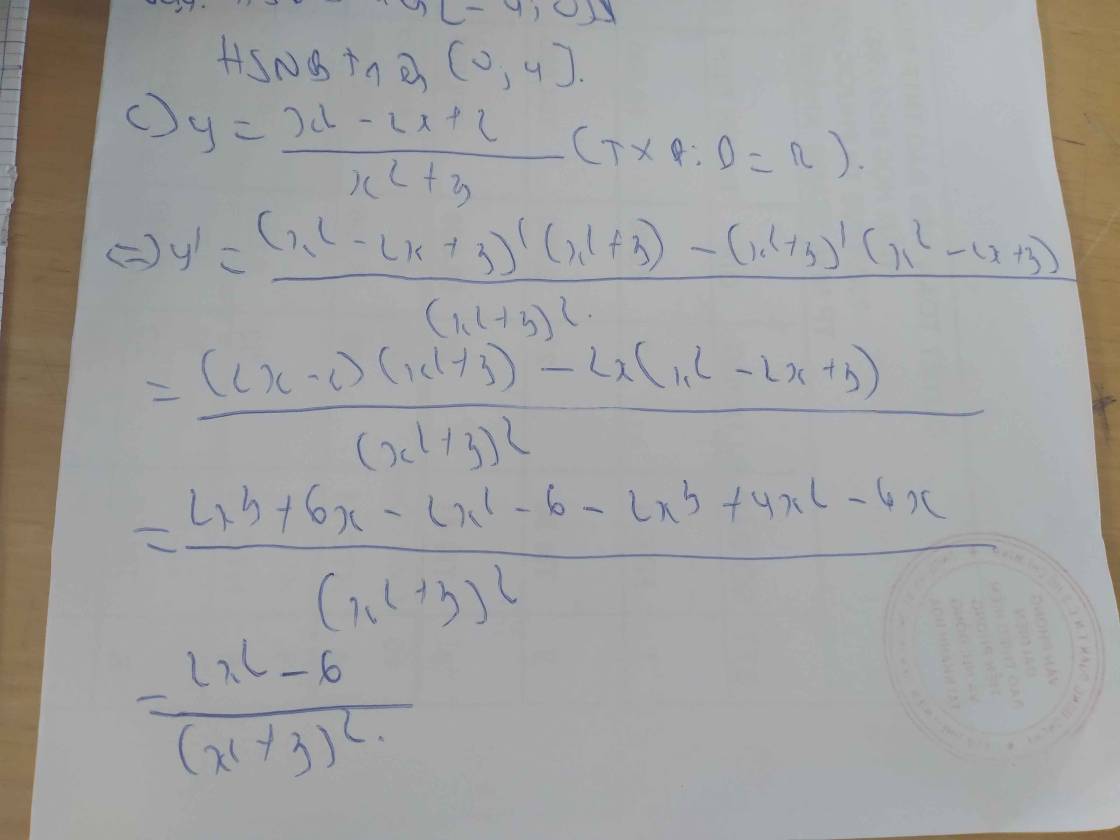\(\dfrac{2x-3}{\sqrt{x^2-1}}\) nghịch biến trên khoảng nào?

Những câu hỏi liên quan
\(y=\dfrac{2x-3}{\sqrt{x^2-1}}\) nghịch biến trong khoảng nào?
tập xác định \(D=\left(-\infty;-1\right)\cup\left(1;+\infty\right)\)
ta có \(y'=\dfrac{3x-2}{\sqrt{\left(x^2-1\right)^3}}\)
từ đó suy ra hàm số nghịch biến trên:\(\left(-\infty;-1\right)\)
Đúng 0
Bình luận (1)
Lời giải:
$y'=\frac{3x-2}{\sqrt{(x^2-1)^3}}$
\(y'<0\Leftrightarrow \left\{\begin{matrix} 3x-2<0\\ x^2-1>0\end{matrix}\right.\Leftrightarrow x< -1\)
Vậy hàm số nghịch biến trong khoảng $(-\infty ;-1)$
Đúng 0
Bình luận (4)
Cau 1: Hàm số y= \(\frac{x}{\sqrt{x^2-x}}\) nghịch biến trên khoảng nào?
Cau 2: Hàm số y=\(x+\sqrt{2x^2+1}\)nghịch biến trên khoảng nào?
Câu 1: Điều kiện \(D=\left(-\infty;0\right)U\left(1;+\infty\right)\)
\(y'=\frac{\sqrt{x^2-x}-x.\frac{2x-1}{2\sqrt{x^2-x}}}{x^2-x}=\frac{-x}{2\left(x^2-x\right)\sqrt{x^2-x}}\)
Ta thấy \(y'< 0\) trên \(\left(1;+\infty\right)\), suy ra hàm số nghịch biến trên \(\left(1;+\infty\right)\).
Câu 2:
\(y'=1+\frac{2x}{\sqrt{2x^2+1}}=\frac{2x+\sqrt{2x^2+1}}{\sqrt{2x^2+1}}\)
Xét bất phương trình:
\(2x+\sqrt{2x^2+1}< 0\)
\(\Leftrightarrow\sqrt{2x^2+1}< -2x\)
\(\Leftrightarrow\hept{\begin{cases}x< 0\\2x^2+1< 4x^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 0\\x< \frac{-\sqrt{2}}{2}\left(h\right)x>\frac{\sqrt{2}}{2}\end{cases}}\Leftrightarrow x< \frac{-\sqrt{2}}{2}\)
Vậy hàm số nghịch biến trên \(\left(-\infty;\frac{-\sqrt{2}}{2}\right)\).
Cho hàm số y = \(\sqrt{2x^2+1}\) Khẳng định nào đúngA: HS đồng biến trên khoảng (0;\(+\infty\))B: HS đồng biến trên khoảng (-\(\infty\);0)C: HS nghịch biến trên khoảng(0;+\(\infty\))D: HS nghịch biến trên khoảng(-1;1)
Xem chi tiết
Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.
Đúng 1
Bình luận (1)
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)
Khoảng nghịch biến của hàm số y= 1/2x^4-3x^2-3 là gì các bạn?
Hàm số y= x^2/1-x đồng biến trên khoảng nào?
Hàm số y= x^3+3x^2 nghịch biến trên khoảng nào?
y=\(\dfrac{2+3x}{\sqrt{5}}\)
y=\(\dfrac{3x+1}{2}-\dfrac{x-1}{3}\)
hàm số nào đồng biến hàm số nào nghịch biến trên R
Hàm số y = \(\sqrt{2x-x^{^2}}\) nghịch biến trên khoảng nào sau?
A. (0;1)
B. (0;2)
C. (1;2)
D. (1;+∞)
Lời giải:
TXĐ: $[0;2]$. Hàm nghịch biến khi \(y'=\frac{1-x}{\sqrt{2x-x^2}}<0\Leftrightarrow \left\{\begin{matrix} 1-x< 0\\ 2x-x^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>1\\ 0< x< 2\end{matrix}\right.\)
$\Leftrightarrow 1< x< 2$
Đáp án C.
Đúng 1
Bình luận (0)
xét tính đồng biến nghịch biến của các hàm số trên
\(y=f\left(x\right)=x^2-2x+3\) trên khoảng \(_{\left(1;+\infty\right)}\)
y=f(x)=\(\sqrt{3-x}\) trên khoảng \(\left(-\infty;3\right)\)
tìm khoảng đồng biến nghịch biến
a) \(y=\sqrt{4x-x^2}\)
b) \(y=\sqrt{16-x^2}\)
c) \(y=\dfrac{x^2-2x+2}{x^2+3}\)