ta có: a3+b3>(=)ab(a+b); c3+a3>(=)ca(c+a)
\(\Rightarrow\frac{1}{2a^3+b^3+c^3+2}\le\frac{bc}{\left(b+c\right)\left(a+b+c\right)}\le\frac{b+c}{4\left(a+b+c\right)}\)
tương tự =>đpcm
chứng minh :
a3 +b3 =(a+b).(a2 -ab +b2)
a3 -b3 =(a-b).(a2 +ab +b2)
VP `=(a+b)(a^2-ab+b^2)`
`=a^3-a^2b+ab^2+a^2b-ab^2+b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)+b^3`
`=a^3+b^3`
.
VP `=(a-b)(a^2+ab+b^2)`
`=a^3+a^2b+ab^2-a^2b-ab^2-b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)-b^3`
`=a^3-b^3`
Ta có: \(a^3+b^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2+2ab+b^2-3ab\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)\)
Ta có: \(a^3-b^3\)
\(=\left(a-b\right)^3+3ab\left(a-b\right)\)
\(=\left(a-b\right)\left(a^2-2ab+b^2+3ab\right)\)
\(=\left(a-b\right)\left(a^2+ab+b^2\right)\)
Chứng minh:
a) ( a 2 - ab + b 2 ) ( a + b ) = a 3 + b 3 ;
b) ( a 3 + a 2 b + ab 2 + b 3 ) ( a - b ) = a 4 - b 4 ;
Thực hiện phép nhân đa thức với đa thức ở vế trái.
=> VT = VP (đpcm)
Câu 3.5. Giả sử ta muốn tính giá trị trong ô C2 nhân với tổng giá trị trong các ô B3 và A3. Công thức nào sau đây là đúng?
a. C2 . (B3+A3) b. =C2*(B3+A3)
c. =C2(B3+A3) d. C2*B3+A3
2. Chứng minh rằng:
a. a3+ b3 = (a + b)3 - 3ab (a + b)
b. a3+ b3 + c3 - 3abc = (a + b + c) (a2 + b2 c2 - ab - bc - ca)
a )
`VP= (a+b)^3-3ab(a+b)`
`=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2`
`=a^3+b^3 =VT (đpcm)`
b)
b) Ta có
`VT=a3+b3+c3−3abc`
`=(a+b)3−3ab(a+b)+c3−3abc`
`=[(a+b)3+c3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)2+c2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a2+b2+2ab+c2−ac−bc−3ab)`
`=(a+b+c)(a2+b2+c2−ab−bc−ca)=VP`
a) Ta có:
`VP= (a+b)^3-3ab(a+b)`
`=a^3 + b^3+3ab ( a + b )- 3ab ( a + b )`
`=a^3 + b^3=VT(dpcm)`
b) Ta có
`VT=a^3+b^3+c^3−3abc`
`=(a+b)^3−3ab(a+b)+c^3−3abc`
`=[(a+b)^3+c^3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)^2+c^2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a^2+b^2+2ab+c^2−ac−bc−3ab)`
`=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=VP`
Cho hệ phương trình ( a + b ) x + ( a - b ) y = 2 ( 1 ) ( a 3 + b 3 ) x + a 3 - b 3 y = 2 ( a 2 + b 2 ) ( 2 )
Với a ≠ ± b , a b ≠ 0 hệ có nghiệm duy nhất bằng:
![]()
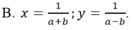
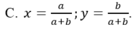
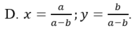
Phân tích đa thức thành nhân tử:
A= x.(y2 - z2) + y.(z2 - x2) + z.(x2 - y2).
B= a.(b3 - c3) + b.(c3 - a3) + c.(a3 - b3).
C= ab.(a + b) - bc.(b + c) + ac. (a - c).
\(A=x\left(y^2-z^2\right)+y\left(z^2-x^2\right)+z\left(x^2-y^2\right)=x\left(y^2-z^2\right)+y\left(-y^2+z^2-x^2+y^2\right)+z\left(x^2-y^2\right)=\left(y^2-z^2\right)\left(x-y\right)+\left(x^2-y^2\right)\left(z-y\right)=\left(y-z\right)\left(y+z\right)\left(x-y\right)-\left(x-y\right)\left(x+y\right)\left(y-z\right)=\left(x-y\right)\left(y-z\right)\left(y+z-x-y\right)=\left(x-y\right)\left(y-z\right)\left(z-x\right)\)
\(B=a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)=ab^3-ac^3+bc^3-a^3b+a^3c-b^3c=ab\left(b^2-a^2\right)-c^3\left(a-b\right)+c\left(a^3-b^3\right)=-ab\left(a-b\right)\left(a+b\right)-c^3\left(a-b\right)+c\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)\left(-a^2b-ab^2-c^3+a^2c+abc+b^2c\right)\)
\(C=ab\left(a+b\right)-bc\left(b+c\right)+ac\left(a-c\right)=ab\left(a+b\right)-bc\left(a+b-a+c\right)+ac\left(a-c\right)=ab\left(a+b\right)-bc\left(a+b\right)+bc\left(a-c\right)+ac\left(a-c\right)=b\left(a+b\right)\left(a-c\right)+c\left(a-c\right)\left(a+b\right)=\left(a+b\right)\left(c+c\right)\left(a-c\right)\)
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
\(5,M=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\\ M=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\\ M=1\left(1-3ab\right)=1-3ab\ge1-\dfrac{3\left(a+b\right)^2}{4}=1-\dfrac{3}{4}=\dfrac{1}{4}\\ M_{min}=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
giải giúp mìnhh
Câu 5:
\(a+b=1\Rightarrow a=1-b\)
\(M=a^3+b^3=\left(1-b\right)^3+b^3=1-3b+3b^2-b^3+b^3\)
\(=1-3b+3b^2=3\left(b^2-b+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(b-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
\(minM=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)
Câu 7:
\(a^3+b^3+abc\ge ab\left(a+b+c\right)\)
\(\Leftrightarrow a^3+b^3+abc-ab\left(a+b+c\right)\ge0\)
\(\Leftrightarrow a^3+b^3-a^2b-ab^2\ge0\)
\(\Leftrightarrow a^2\left(a-b\right)-b^2\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)(đúng do a,b dương)
Dấu "=" xảy ra \(\Leftrightarrow a=b\)
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
5.
Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow2a^2+2b^2\ge a^2+b^2+2ab\)
\(\Rightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2=\dfrac{1}{2}\)
\(M=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=a^2+b^2-ab\)
\(M=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\left(a+b\right)^2=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\ge\dfrac{3}{2}.\dfrac{1}{2}-\dfrac{1}{2}=\dfrac{1}{4}\)
\(M_{min}=\dfrac{1}{4}\) khi \(a=b=\dfrac{1}{2}\)
6.
Do \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=2>0\)
Mà \(a^2-ab+b^2>0\Rightarrow a+b>0\)
Mặt khác với mọi a;b ta có:
\(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow a^2+b^2+2ab\ge4ab\)
\(\Rightarrow\left(a+b\right)^2\ge4ab\Rightarrow ab\le\dfrac{1}{4}\left(a+b\right)^2\) \(\Rightarrow-ab\ge-\dfrac{1}{4}\left(a+b\right)^2\)
Từ đó:
\(2=a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\ge\left(a+b\right)^3-3.\dfrac{1}{4}\left(a+b\right)^2\left(a+b\right)=\dfrac{1}{4}\left(a+b\right)^3\)
\(\Rightarrow\left(a+b\right)^3\le8\Rightarrow a+b\le2\)
\(N_{max}=2\) khi \(a=b=1\)
7.
Ta có:
\(a^3+b^3+abc=\left(a+b\right)\left(a^2+b^2-ab\right)+abc\ge\left(a+b\right)\left(2ab-ab\right)+abc\)
\(\Rightarrow a^3+b^3+abc\ge ab\left(a+b\right)+abc=ab\left(a+b+c\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b\)
8.
\(\left|a+b\right|>\left|a-b\right|\Leftrightarrow\left(a+b\right)^2>\left(a-b\right)^2\)
\(\Leftrightarrow a^2+2ab+b^2>a^2-2ab+b^2\)
\(\Leftrightarrow4ab>0\Leftrightarrow ab>0\)
\(\Rightarrow a;b\) cùng dấu
Tính giá trị biểu thức :
A = [ (a+b)2019 - c2019 ] [ (b+c)2019 - a2019 ] [ (a+c)2019 - b2019 ]