Cho mặt cầu S(O;R) và điểm A cố định với OA = d > R. Qua A kẻ đường thẳng ∆ tiếp xúc với mặt cầu S(O;R) tại M. Độ dài đoạn thẳng AM là:
A. d 2 + R 2 B. 2 R 2 - d 2
C. R 2 - 2 d 2 D. d 2 - R 2
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = AC = 6, BC = 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng
A. 404 π 5
B. 2916 π 5 75 .
C. 404 π 505 75
D. 324 π 5
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho A B = 3 , A C = 4 , B C = 5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
A. 7 21 π 2
B. 13 13 π 6
C. 20 5 π 3
D. 29 29 π 6
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB=3, AC=4, BC=5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng
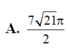
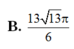
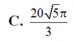
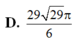
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
A. h ≤ R
B. h ≥ R
C. h > R
D. h < R
Đáp án D
Từ vị trí tương đối của một mặt phẳng với mặt cầu ta có đáp án đúng là D.
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu:
A. h < R
B. h = R
C. h ≤ R
D. h ≥ R
Đáp án D
Từ vị trí tương đối của một mặt phẳng và mặt cầu ta có mặt phẳng (P) có điểm chung với mặt cầu (S) khi và chỉ khi mặt phẳng (P) tiếp xúc hoặc cắt mặt cầu (S).
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Chọn C.
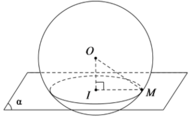
*) Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
*) Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên ![]()
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Chọn C.
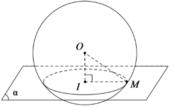
Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
Khi d < R thì mặt phẳng cắt mặt cầu (S) theo giao tuyến là đường tròn tâm I bán kính r = IM.
Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên
![]()
Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?
A. 4 π R 2
B. 4 R 2
C. 4 3 π R 2
D. π R 2
Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?
A. 4 πR 2
B. 4 R 2
C. 4 3 πR 2
D. πR 2
Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?
A . 4 πR 2
B . 4 R 2
C . 4 3 πR 2
D . πR 2