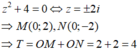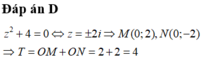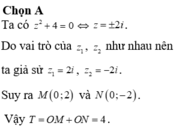Gọi O là gốc tọa độ; A là điểm có tọa độ (-2;3). Xác định các hệ số a, b để đường thẳng y = ax + b đi qua điểm B(2;1) và song song với đường thẳng OA

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho parabol (P):y=x2 . Gọi A, B là hai điểm trên parabol có
hoành độ tương ứng là 1 và 2. Tìm tọa độ hình chiếu vuông góc của gốc tọa độ O lên đường
thẳng AB.
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
Đúng 0
Bình luận (0)
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
4
0.
Gọi M, N là các điểm biểu diễn của các số phức
z
1
,
z
2
trên mặt phẳng tọa độ. Tính T OM + ON với O là gốc tọa độ. A. ...
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 4 = 0. Gọi M, N là các điểm biểu diễn của các số phức z 1 , z 2 trên mặt phẳng tọa độ. Tính T = OM + ON với O là gốc tọa độ.
A. T = 2 2 .
B. T = 8
C. T = 2
D. T = 4
Gọi
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
4
0
. Gọi M, N là các điểm biểu diễn của các số phức
z
1
,
z
2
trên mặt phẳng tọa độ. Tính T OM + ON với O là gốc tọa độ A.
T
2
2
B....
Đọc tiếp
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 4 = 0 . Gọi M, N là các điểm biểu diễn của các số phức z 1 , z 2 trên mặt phẳng tọa độ. Tính T = OM + ON với O là gốc tọa độ
A. T = 2 2
B. T = 8
C. T = 2
D. T = 4
Trong mặt phẳng tọa độ Oxy, cho parabol (P) y= x2 và đường thẳng (d): y=2x+3
Gọi A,B là tọa độ giao điểm của (d) và (P) . Tính diện tích tam giác OAB ( O là gốc tọa độ )
Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
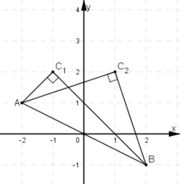
B đối xứng với A qua O ⇒ O là trung điểm của AB
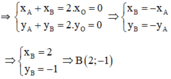
C có tung độ bằng 2 nên C(x; 2)
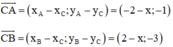
Tam giác ABC vuông tại C
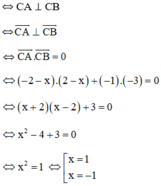
Vậy có hai điểm C thỏa mãn là C1(1; 2) và C2(–1; 2).
Đúng 0
Bình luận (0)
Kí hiệu
z
1
;
z
2
là hai nghiệm phức của phương trình
z
2
+
4
0
. Gọi M, N lần lượt là các điểm biểu diễn của
z
1
;
z
2
trên mặt phẳng tọa độ. Tính T OM + ON với O là gốc tọa độ A. T 4 B. T 2 C. T
2...
Đọc tiếp
Kí hiệu z 1 ; z 2 là hai nghiệm phức của phương trình z 2 + 4 = 0 . Gọi M, N lần lượt là các điểm biểu diễn của z 1 ; z 2 trên mặt phẳng tọa độ. Tính T = OM + ON với O là gốc tọa độ
A. T = 4
B. T = 2
C. T = 2 2
D. T = 8
Kí hiệu
z
1
,
z
2
là hai nghiệm của phương trình
z
2
+
4
0
. Gọi M, N lần lượt là các điểm biểu diễn của số phức
z
1
,
z
2
trên mặt phẳng tọa độ. Giá trị TOM+ON với O là gốc tọa độ là: A.
T
2...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm của phương trình z 2 + 4 = 0 . Gọi M, N lần lượt là các điểm biểu diễn của số phức z 1 , z 2 trên mặt phẳng tọa độ. Giá trị T=OM+ON với O là gốc tọa độ là:
A. T = 2
B. T = 2
C. T = 8
D. T = 4
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC A. 1372/9 B. 686/9 C. 524/3 D. 343/9
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. 686/9
C. 524/3
D. 343/9
Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: ![]()
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận ![]() làm VTPT.
làm VTPT.
Do đó (P) có phương trình:
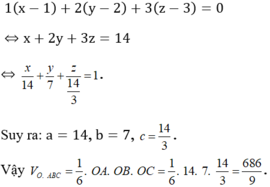
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm Mvà cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A,B,C. Tính thể tích khối chóp O.ABC. A.
1372
9
.
B.
686
9
.
C.
524
3
.
D.
343
9...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm Mvà cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A,B,C. Tính thể tích khối chóp O.ABC.
A. 1372 9 .
B. 686 9 .
C. 524 3 .
D. 343 9 .