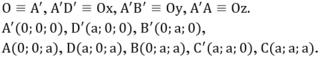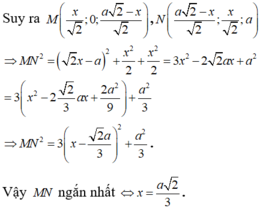Cho x,y,z thuộc đoạn [0;1] và x+y+z=1 tìm GTLN của A=√(8x^2+1)+√(8z^2+1)+√(8y^2+1)

Những câu hỏi liên quan
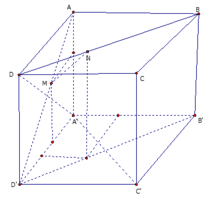
Cho hình lập phương ABCD.ABCD cạnh bằng a. Lấy điểm M thuộc đoạn AD, điểm N thuộc đoạn BD sao cho AM DN x, (0 x a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
A
.
x
a
2
3
B
.
x
a
2
4
C
....
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
A . x = a 2 3
B . x = a 2 4
C . x = a 3
D . x = a 2
cho x,y,z thuộc Q* và x-y+z=0. cmr xy+yz-zx>=0
tìm x,y thuộc Z: (x-1)2016+(y^2-1)2014+| x+y+z|=0
Cho ba số a;b;x thuộc Z và ax - by chia hết cho ( x + y ) . Chứng tỏ ay - bx chia hết cho ( x + y ) , biết rằng ( x + y ) khác 0 .
Giả sử ay - bx chia hết cho x+y
Mà ax-by chia hết cho x+y
=>(ax-by)+(ay-bx) chia hết cho x+y
=> ax-by+ay-bx chia hết cho x+y
=> (ax+ay)-(bx+by) chia hết cho x+y
=> a(x+y)-b(x+y) chia hết cho x+y
=> (a-b)(x+y) chia hết cho x+y (đúng)
=> giả sử đúng
Vậy ay-bx chia hết cho x+y
Đúng 0
Bình luận (0)
Ta có: (a - b)(x + y) luôn chia hết cho (x + y)
Theo giả thiết ax - by chia hết cho (x + y)
=> (a - b) (x + y) - (ax - by) chia hết cho (x + y)
=> ax + ay -bx -by - ax + by chia hết cho (x + y)
=> ay - bx chia hết cho 9x + y)
(ĐPCM)
Đúng 0
Bình luận (0)
Cho x, y thuộc Z. Hãy chứng tỏ rằng:
a, nếu x - y > 0 thì x > y
b, nếu x > y thì x - y > 0
Cho các số hữu tỉ : \(x=\frac{a}{b};y=\frac{c}{d};z=\frac{a+c}{b+d}\)(a,b,c,d thuộc Z ;b>0 ;d>0 ). Chứng minh rằng;nếu x<y thì x<z<y
TÌM x, y, z, thuộc Q biết:
a,I x+1/2I+I y-3/4I+I z+1I=0
\(\left|x+\frac{1}{2}\right|+\left|y-\frac{3}{4}\right|+\left|z+1\right|=0\)
\(\Rightarrow\hept{\begin{cases}\left|x+\frac{1}{2}\right|=0\\\left|y-\frac{3}{4}\right|=0\\\left|z+1\right|=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=0-\frac{1}{2}\\y=0+\frac{3}{4}\\z=0-1\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{-1}{2}\\y=\frac{3}{4}\\z=-1\end{cases}}\)
tìm x,y thuộc Z , biết
x + 45 - 40 + y + 10 -11 < hoặc = 0
Có phải đề là |x+ 45 - 40| + |y + 10 - 11| \(\le\) 0
Đúng 0
Bình luận (0)
|x + 45 - 40| + |y +10 - 11| \(\le\) 0
|x + 45 - 40| ; |y+ 10 - 11| \(\ge\) 0
< = > |x + 45 - 40| = |y + 10 - 11| = 0
< = > |x + 5| = |y - 1| = 0
x + 5 = 0 => x= -5
y - 1 = 0 => y= 1
Vậy x = -5 ; y= 1
Đúng 0
Bình luận (0)
| x + 45 - 40| + |y + 10 - 11| < 0
=> | x + 5 | + |y - 1| < 0
Mà | x + 5 | > 0; | y - 1 | > 0
=> | x + 5 | + | y - 1 | = 0 (không thể < 0)
=> x + 5 = y - 1 = 0
=> x = -5; y=1.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 2 : Tìm x , y thuộc z :
| x | + | y | + | z | = 0
x=0; y=0 ; x =0 . Tích nhé  hồng nguyen thi
hồng nguyen thi
Đúng 0
Bình luận (0)
Các bạn giải chi tiết , nhanh và đúng thì mình tick nhé .
Đúng 0
Bình luận (0)