Cho b, c là các số khác 0 thỏa mãn đồ thị hàm số \(y=x^2+bx+c\) đi qua điểm A (1;0) và có đỉnh I có tung độ bằng -1. Khi đó giá trị b.c = ...

Những câu hỏi liên quan
tìm m thỏa mãn yêu cầu bài toána) đồ thị hàm số ydfrac{x+3}{2x+3m} có đường tiệm cận đứng đi qua điểm M (3;-1)b) đường thẳng x -2 là tiệm cận đứng của đồ thị hàm số ydfrac{2x-3}{x+m}c) biết đồ thị hàm số ydfrac{ax+1}{bx-2} có tiệm cận đứng là x 2 và tiệm cận ngang y 3. Tính 2a+3bd) đồ thị hàm số ydfrac{x+2}{x^2+2x+m^2-3m} có 2 đường tiệm cận đứng
Đọc tiếp
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) có đường tiệm cận đứng đi qua điểm M (3;-1)
b) đường thẳng x = -2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
c) biết đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có tiệm cận đứng là x = 2 và tiệm cận ngang y = 3. Tính 2a+3b
d) đồ thị hàm số \(y=\dfrac{x+2}{x^2+2x+m^2-3m}\) có 2 đường tiệm cận đứng
a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3
Đúng 0
Bình luận (0)
cho hàm số y = ax^2 + bx + c(a khác 0). tìm a, b, c biết hàm số đó có gtln = 5 khi x = -2 và đồ thị đi qua M(1;-1)
\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...
Đúng 2
Bình luận (0)
Cho các số thực a, b, c thỏa mãn
a
+
c
b
+
1
a
+
b
+
c
+
1...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a + c > b + 1 a + b + c + 1 < 0 . Tìm số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c và trục Ox
A. 0
B. 2
C. 3
D. 1
Đáp án C
Phương pháp giải:
Chọn hệ số a, b, c hoặc đánh giá tích để biện luận số nghiệm của phương trình
Lời giải:
Cách 1. Ta có: 
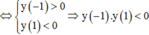
Lại có 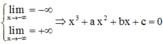 có 3 nghiệm thuộc khoảng
có 3 nghiệm thuộc khoảng ![]()
Cách 2. Chọn 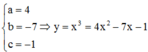 và đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt
và đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt
Đúng 0
Bình luận (0)
Cho a, b, c thỏa mãn
-
1
+
a
-
b
+
c
0
8
+
4
a
+
2
b
+
c...
Đọc tiếp
Cho a, b, c thỏa mãn - 1 + a - b + c > 0 8 + 4 a + 2 b + c < 0 thì số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c với trục Ox là:
A. 1
B. 2
C. 3
D. 0
Đáp án C.
lim x → - ∞ y = - ∞ ( 1 ) f ( - 1 ) = - 1 + a 2 - b + c > 0 ( 2 ) f ( 2 ) = 8 + 4 a 2 + 2 a + c < 0 ( 3 ) lim x → - ∞ y = + ∞ ( 4 )
Từ (1) và (2) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên - ∞ ; - 1 .
Từ (2) và (3) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên - 1 ; 2 .
Từ (3) và (4) ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm trên 2 ; + ∞ .
Do f (x) =0 là phương trình bậc 3 ⇒ Có nhiều nhất 3 nghiệm
⇒ Đường thẳng cắt trục Ox tại 3 điểm phân biệt.
Đúng 0
Bình luận (0)
Cho a, b, c thỏa mãn
−
1
+
a
−
b
+
c
0
8
+
4
a
+
2...
Đọc tiếp
Cho a, b, c thỏa mãn − 1 + a − b + c > 0 8 + 4 a + 2 b + c < 0 thì số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c với trục Ox là
A. 1
B. 2
C. 3
D. 0
Cho các số thực a, b, c thỏa mãn
a
−
b
+
c
1
a
+
b
+
c
−
1
. S...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a − b + c > 1 a + b + c < − 1 . Số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c và trục hoành là
A. 0
B. 1
C. 2
D. 3
Đáp án D.
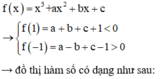
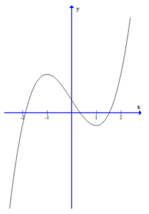
Đồ thị hàm số cắt trục hoành tại 3 điểm.
Đúng 0
Bình luận (0)
Cho các số thực a, b, c thỏa mãn
a
−
b
+
c
1
a
+
b
+
c
−
1
. S...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a − b + c > 1 a + b + c < − 1 . Số giao điểm của đồ thị hàm số y = x 3 + a x 2 + b x + c và trục hoành là
A. 0.
B. 1.
C. 2.
D. 3.
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
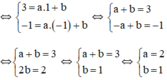
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
Cho hàm số y = ax + b .Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:
a) Đi qua hai điểm A(1; 3) và B(-1; -1).
b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).
a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
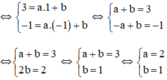
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.
Đúng 0
Bình luận (0)
c1: cho hàm số y-2xa) vẽ đồ thị hàm sốb)tìm tọa độ các điểm thuộc đồ thị hàm số có tung độ bằng hoành độc2: a, cho các số a,b,c khác 0 thỏa mãn a-b+c/2b c-a+b/2a a-c+b/2cb, tìm giá trị biểu thức P(1+c/b) x (1+b/a) x (1+a/c) c3: tìm x bt: 2018 x | x-1| + (x-1)^2 2019 x |1-x|chú ý c3 x số 1 và số 4 là dấu nhânBÀI 1: cho tam giác ABC nhọn, AH vuông góc với BC, H thuộc BC, P thuộc tia đối HA sao cho HAHD. Chứng minh:a, tam giác ABC tam giác DBCb, CB là tia phân giác góc ACDBÀI 2: Tìm X,Y,Z thỏa mã...
Đọc tiếp
c1: cho hàm số y=-2xa) vẽ đồ thị hàm sốb)tìm tọa độ các điểm thuộc đồ thị hàm số có tung độ bằng hoành độc2: a, cho các số a,b,c khác 0 thỏa mãn a-b+c/2b= c-a+b/2a =a-c+b/2cb, tìm giá trị biểu thức P=(1+c/b) x (1+b/a) x (1+a/c) c3: tìm x bt: 2018 x | x-1| + (x-1)^2 = 2019 x |1-x|chú ý c3 x số 1 và số 4 là dấu nhânBÀI 1: cho tam giác ABC nhọn, AH vuông góc với BC, H thuộc BC, P thuộc tia đối HA sao cho HA=HD. Chứng minh:a, tam giác ABC = tam giác DBCb, CB là tia phân giác góc ACDBÀI 2: Tìm X,Y,Z thỏa mãn |3x-2y|2014+(5y-4z)^2016+|x^2-y^2+z^2+145|=0 BÀI 3: Tìm ba số A,B,C bt:a và b lần lượt tỉ lệ thuận với 7 và 11 b và c lần lượt tỉ lệ nghịch với 3 và 8 a-b+c=1













