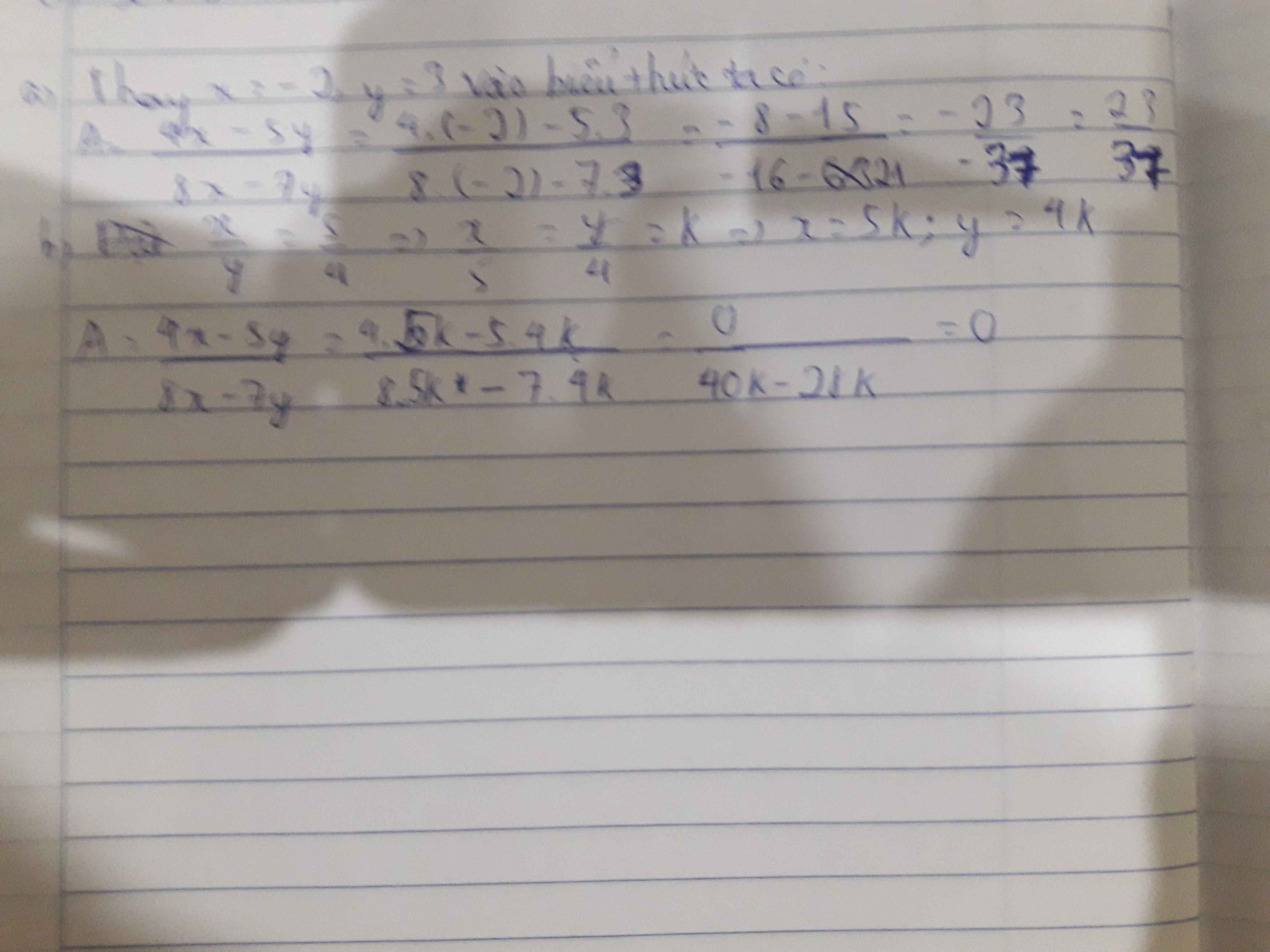Cho biểu thức: f(x)=x2-4x=3
a,Tính giá trị của biểu thức f(x) tại x=0; x=1; x=3
b,Giá trị x nào là nghiệm của đa thức f(x)? Vì sao?

Những câu hỏi liên quan
Giá trị của biểu thức đã cho tại x = 1
Giá trị của biểu thức đã cho tại x = 10
: Giá trị của biểu thức đã cho tại x = 1 phần 2
: Giá trị của biểu thức đã cho tại x = âm 3 phần 2
Giá trị của biểu thức đã cho tại x= -1
Biểu thức đâu hở bạn
Biểu thức đâu bạn
Đề đâu??????
Xem thêm câu trả lời
Cho biểu thức : A=\(\left(\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
a, Rút gọn biểu thức A
b, Tính giá trị biểu thức A tại x, biết \(x=-\dfrac{1}{2}\)
c, Tính giá trị của x để A<0
a, ĐKXĐ: x≠±3
A=\(\left(\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{3-x}{x+3}.\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{3-x}{x-3}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{9-x^2}{x^2-9}+\dfrac{x^2-3x}{x^2-9}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{-3}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\dfrac{-1}{x^2}\)
b, Thay x=\(-\dfrac{1}{2}\) (TMĐKXĐ) vào A ta có:
\(\dfrac{-1}{\left(-\dfrac{1}{2}\right)^2}\)=-4
c, A<0 ⇔ \(\dfrac{-1}{x^2}< 0\) ⇔ x2>0 (Đúng với mọi x)
Vậy để A<0 thì x đúng với mọi giá trị (trừ ±3)
Đúng 1
Bình luận (0)
Cho biểu thức: A=\(\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
a, Rút gọn biểu thức A
b, Tính giá trị biểu thức A tại x, biết |x|=\(\dfrac{1}{2}\)
c, Tìm giá trị của x để A<0
Cho biểu thức: A=\(\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right)\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
a, Rút gọn biểu thức A
b, Tính giá trị biểu thức A tại x, biết |x|=\(\dfrac{1}{2}\)
c, Tìm giá trị của x để A<0
a, ĐKXĐ: x≠±2
A=\(\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right)\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
A=\(\left(\dfrac{x}{x^2-4}-\dfrac{2x+4}{x^2-4}+\dfrac{x-2}{x^2-4}\right)\left(\dfrac{x^2+2x}{x+2}-\dfrac{2x+4}{x+2}+\dfrac{10-x^2}{x+2}\right)\)
A=\(\left(\dfrac{-6}{x^2-4}\right)\left(\dfrac{6}{x+2}\right)\)
A=\(\dfrac{-36}{\left(x-2\right)\left(x+2\right)^2}\)
b, |x|=\(\dfrac{1}{2}\)
TH1z: x≥0 ⇔ x=\(\dfrac{1}{2}\) (TMĐKXĐ)
TH2: x<0 ⇔ x=\(\dfrac{-1}{2}\) (TMĐXĐ)
Thay \(\dfrac{1}{2}\), \(\dfrac{-1}{2}\) vào A ta có:
\(\dfrac{-36}{\left(\dfrac{1}{2}-2\right)\left(\dfrac{1}{2}+2\right)^2}\)=\(\dfrac{96}{25}\)
\(\dfrac{-36}{\left(\dfrac{-1}{2}-2\right)\left(\dfrac{-1}{2}+2\right)^2}\)=\(\dfrac{32}{5}\)
c, A<0 ⇔ \(\dfrac{-36}{\left(x-2\right)\left(x+2\right)^2}\) ⇔ (x-2)(x+2)2 < 0
⇔ {x-2>0 ⇔ {x>2
[ [
{x+2<0 {x<2
⇔ {x-2<0 ⇔ {x<2
[ [
{x+2>0 {x>2
⇔ x<2
Vậy x<2 (trừ -2)
Đúng 1
Bình luận (1)
Cho biểu thức: A=\(\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
a, Rút gọn biểu thức A
b, Tính giá trị biểu thức A tại x, biết |x|=\(\dfrac{1}{2}\)
c, Tìm giá trị của x để A<0
Tính giá trị của biểu thức sau: A=4x-5y/8x-7y. a) Tại x=-2, y=3; b) Biết x/y=5/4
a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)
Đúng 3
Bình luận (0)
Cho biểu thức: Aleft(dfrac{2+x}{2-x}-dfrac{4x^2}{x^2-4}-dfrac{2-x}{2+x}right):dfrac{x^2-3x}{2x^2-x^3}Với x≠±2,x≠0,x≠3a, Rút gọn biểu thức Ab,Tính giá trị của A khi x12c, Tính x khi A1d, Tìm x∈Z để A nguyêne, Tìm x để biểu thức A4
Đọc tiếp
Cho biểu thức: \(A=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
Với x≠±2,x≠0,x≠3
a, Rút gọn biểu thức A
b,Tính giá trị của A khi x=12
c, Tính x khi A=1
d, Tìm x∈Z để A nguyên
e, Tìm x để biểu thức A>4
Lời giải:
a.
\(A=\left[\frac{(2+x)^2}{(2-x)(2+x)}+\frac{4x^2}{(2-x)(2+x)}-\frac{(2-x)^2}{(2-x)(2+x)}\right]:\frac{x(x-3)}{x^2(2-x)}\)
\(=\frac{(2+x)^2+4x^2-(2-x)^2}{(2-x)(2+x)}.\frac{x^2(2-x)}{x(x-3)}=\frac{4x(x+2)}{(2-x)(2+x)}.\frac{x^2(2-x)}{x(x-3)}=\frac{4x^2}{x-3}\)
b.
Khi $x=12$ thì $A=\frac{4.12^2}{12-3}=64$
c.
$A=1\Leftrightarrow \frac{4x^2}{x-3}=1$
$\Leftrightarrow 4x^2=x-3$
$\Leftrightarrow 4x^2-x+3=0$
$\Leftrightarrow (2x-\frac{1}{4})^2=-\frac{47}{16}< 0$ (vô lý)
Vậy không tồn tại $x$
d. Để $A$ nguyên thì $\frac{4x^2}{x-3}$ nguyên
$\Leftrightarrow 4x^2\vdots x-3$
$\Leftrightarrow 4(x^2-9)+36\vdots x-3$
$\Leftrightarrow 36\vdots x-3$
$\Leftrightarrow x-3\in\left\{\pm 1;\pm 2;\pm 3;\pm 4;\pm 9; \pm 12; \pm 36\right\}$
Đến đây bạn có thể tự tìm $x$ được rồi, chú ý ĐKXĐ để loại ra những giá trị không thỏa mãn.
e.
$A>4\Leftrightarrow \frac{4x^2}{x-3}>4$
$\Leftrightarrow \frac{x^2}{x-3}>1$
$\Leftrightarrow \frac{x^2-x+3}{x-3}>0$
$\Leftrightarrow x-3>0$ (do $x^2-x+3>0$ với mọi $x$ thuộc ĐKXĐ)
$\Leftrightarrow x>3$. Kết hợp với đkxđ suy ra $x>3$
Đúng 4
Bình luận (0)
a, Cho x+y=1. Tính giá trị của biểu thức x3+y3+3xy
b, Cho x-y=1. Tính giá trị của biểu thức x3-y3-3xy
a.Từ giả thiết:
x+y=1.
=> (x+y)^3=1^3=1
=> x^3 +3x^2.y+3x.y^2+y^3=1(HĐT)
=> x^3+y^3+3xy(x+y)=1
=> x^3+y^3+3xy.1=1
<=> x^3+y^3+3xy=1
b.x3-y3-3xy=x3-y3-3xy.1
Mà x-y=1 nên
x3-y3-3xy=x3-y3-3xy(x-y)
x3-y3-3x2y+3xy2
=(x-y)3=13=1
Đúng 0
Bình luận (0)
Cho biểu thức: A = (x + 1)(x – 2) – x(2x – 3) + 4 + 2x2
a) Chứng minh: A = x2 + 2x + 2
b) Tính giá trị của biểu thức A khi x =
c) Chứng minh biểu thức A luôn dương với mọi x.
a: \(A=\left(x+1\right)\left(x-2\right)-x\left(2x-3\right)+2x^2+4\)
\(=x^2-x-2-2x^2+3x+2x^2+4\)
\(=x^2+2x+2\)
Đúng 3
Bình luận (0)
\(a,A=x^2-x-2-2x^2+3x+4+2x^2=x^2+2x+2\\ c,A=\left(x^2+2x+1\right)+1=\left(x+1\right)^2+1\ge1>0\)
Đúng 2
Bình luận (0)