Cho tam giác ABC cân tại A, H là trung điểm BC, kẻ HE vuông góc AC tại E; HF vuông góc AB tại F
1. CMR tam giác ABH = tam giác ACH
2. CMR tam giác AEF cân
3. CMR EF song song BC
cho tam giác ABC cân tại A , H là trung điểm BC
a) chứng minh tam giác AHB = tam giác AHC
b) chứng minh AH ⊥ BC
kẻ HE vuông góc AB tại E
HF vuông góc AC tại F
a, tam giac ABC can tai A (gt) => AB = AC va goc ABC = goc ACB (dn)
xet tamgiac ABH va tam giac ACH co : BH = HC do H la trung diem cua BC (gt)
=> tam giac ABH = tam giac ACH (c - g - c)
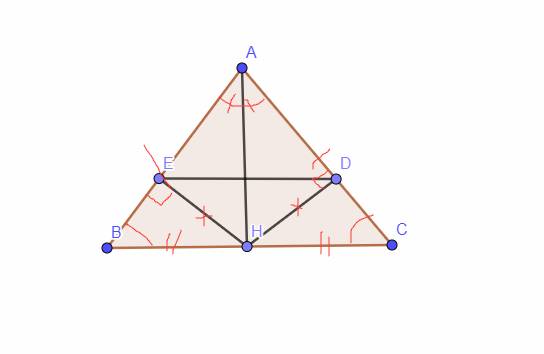
cho tam giác cân ABC cân tại A. Gọi H là trung điểm BC. a. chứng minh góc BAH = góc CAH. b. Kẻ HE vuông góc AB (E thuộc AB). Kẻ HD vuông góc AC (D thuộc AC). Chứng minh HDE là tam giác cân
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `BAH` và Tam giác `CAH` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`HB = HC ( H` là trung điểm của `BC)`
`=> \text {Tam giác BAH = Tam giác CAH (c-g-c)}`
`->`\(\widehat{BAH}=\widehat{CAH} (\text {2 góc tương ứng})\)
`b,` Xét Tam giác `HEA` và Tam giác `BDA` có:
`AH` chung
\(\widehat{EAH}=\widehat{DAH} (a)\)
\(\widehat{HEA}=\widehat{HDA}=90^0\)
`=> \text {Tam giác HEA = Tam giác BDA (ch-gn)}`
`-> HE = HD (\text {2 cạnh tương ứng})`
`\text {Xét Tam giác HDE: HD = HE} -> \text {Tam giác HDE cân tại H}`
cho tam giác abc cân tại a gọi h là trung điểm của bc
a, Chứng minh AH vuông góc với BC
b, Kẻ HE vuong góc với AB tại E ; HF vuông góc với AC tại F . Chứng minh HE = HF
c, Chứng minh tam giác AEF là tam giác cân
d, Chứng minh EF song song BC
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
1) Chứng minh tam giác ABH = tam giác ACH và H là trung điểm của BC.
2) Nếu có AB = 10cm, BC = 12 cm, hãy tính độ dài đoạn thẳng AH.
3) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Lấy các điểm M và N sao cho E là trung điểm của HM, F là trung điểm của HN. Chứng minh AN = AH.
4) Tam giác ABC cần thêm điều kiện gì thì A là trung điểm của MN?
Giúp mik vs ạ mik đang cần gấp.
1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
2: Ta có: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=64\)
=>\(HA=\sqrt{64}=8\left(cm\right)\)
3: Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AH
4: Xét ΔAHM có
AE là đường trung tuyến
AE là đường cao
Do đó: ΔAHM cân tại A
=>AM=AH
Ta có: ΔAHN cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAN
=>\(\widehat{HAN}=2\cdot\widehat{HAC}\)
Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
=>\(\widehat{HAM}=2\cdot\widehat{HAB}\)
Ta có: AM=AH
AH=AN
Do đó: AM=AN
Ta có: \(\widehat{HAM}+\widehat{HAN}=\widehat{MAN}\)
=>\(\widehat{MAN}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{MAN}=2\cdot\widehat{BAC}\)
Để A là trung điểm của MN thì AM=AN và góc MAN=180 độ
=>góc MAN=180 độ
=>\(2\cdot\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=90^0\)
Cho tam giác ABC vuông cân với đáy BC . Gọi M và n lần lượt là trung điểm của AB và AC . Kẻ NH vuông góc với CM tại H . Kẻ HE vuông góc với AB tại E . CMR tam giác ABH cân
Cho tam giác ABC vuông tại A có AB < AC. Trên cạnh BC lấy điểm H sao cho HB = BA, từ H kẻ HE vuông góc với BC tại H (E thuộc AC)
a) Chứng minh:
b) Chứng minh: Tam giác AEH cân tại E.
c) Chứng minh: BE là đường trung trực của AH.
d) Gọi K là giao điểm của HE và BA. Chứng minh: BE vuông góc KC
câu a là trứng minh tam giac abe và hbe nhé
\
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
Do đó; ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
Do đó: E là trực tâm
=>BE vuông góc KC
B1 :Cho tam giác ABC có 2 đường cao BD,CE. Gọi M,N là trung điểm của BC,DE. C/m MN vuông góc DE.
B2: Cho tam giác ABC cân tại A. H là trung điểm của BC. Kẻ HE vuông góc AC. Gọi I là trung điểm của HE. C/m AI vuông góc BE
B3: Cho tam giác ABC vuông tại A. M là trung điểm của BC. Đường cao AH. Kẻ HE vuông góc AC cắt AM tại N. C/m AM vuông góc BN
Cho tam giác ABC cân tại A. Gọi H là trung điểm BC. Từ H kẻ HD vuông góc AB tại D và HE vuông góc với AC tại E. a/ Chứng minh: tam giac HDB = tam giacHEC b/ Chứng minh : AD=AE. c/ Qua A kẻ đường thẳng xy song song BC, tia HD cắt xy tại M, tia HE cắt xy tại N. Chứng minh tam giác HMN là tam giác cân?
giup tui voii tks nhieuu
a: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHDB=ΔHEC
b: Ta có: ΔHDB=ΔHEC
nên BD=EC
Ta có: AD+DB=AB
AE+EC=AC
mà BD=CE
và AB=AC
nên AD=AE
Cho tam giác ABC cân tại A (Góc A < 90 độ) Ket AH vuônh góc BC a. CMR : tam giác ABH = tam giác ACH b.CM: AH là phân giác của tam giác ABC c. Từ H kẻ HE vuông góc AB tại E , HF vuông góc AC tại F . Gọi I là giao điểm của EF và AH . CM : AI là trung tuyến của tam giác AEF
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
c: Xet ΔAEH vuôngtại E và ΔAFH vuông tại F có
AH chung
góc EAH=góc FAH
=>ΔAEH=ΔAFH
=>AE=AF
=>ΔAEF cân tại A
mà AI là phân giác
nên AI là trung tuyến