Cho tam giác ABC vuông tại A đường cao AH biết độ dài AH= 12; HB= 16 tìm độ dài các cạnh AB; AC; HC

Những câu hỏi liên quan
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC3cm ,BC6cm . Tính độ dài các đoạn thẳng AB, AC .2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC3:7 , AH42cm.Tính độ dài BH , CH3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB21cm,AC28cm .Tính HD
Đọc tiếp
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC=3cm ,BC=6cm . Tính độ dài các đoạn thẳng AB, AC .
2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:7 , AH=42cm.Tính độ dài BH , CH
3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH=9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC
4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB=21cm,AC=28cm .Tính HD
1. Cho tam giác ABC vuông tại A, biết AH 16, BH 9. Tính AB.2. Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Tính độ dài HB.3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12, BC 15. Tính HC.4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 6, HC 9. Tính độ dài AC.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, BC 16cm. Tính AH6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 8cm, HC 12 cm. Tính AC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (3)
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, BC = 10cm
a) Tính độ dài AC.
b) Tính diện tích tam giác ABC.
c) Tính độ dài đường cao AH.
a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A biết AC=12, BC=15:
a) Giải tam giác ABC
b) Tính độ dài đường cao AH, đường phân giác AD của ΔABC
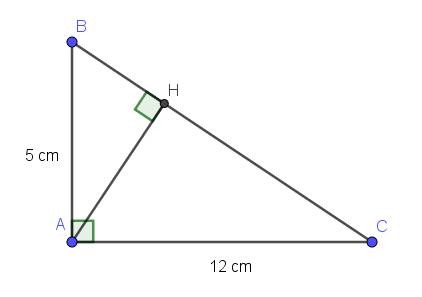
cho tam giác abc vuông tại a, đường cao ah (h thuộc bc) biết ab=5, ac=12 hảy tính độ dài các cạch bh,ch,ah
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=5^2+12^2=169
=>BC=13
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC; AB^2=BH*BC; AC^2=CH*CB
=>AH=5*12/13=60/13; BH=5^2/13=25/13; CH=12^2/13=144/13
Đúng 0
Bình luận (0)
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{5^2}+\frac{1}{12^2}=\frac{169}{3600}$
$\Rightarrow AH=\frac{60}{13}$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-(\frac{60}{13})^2}=\frac{25}{13}$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết BH=9cm,CH=5cm.Tính độ dài đường cao AH?
Áp dụng hệ thức lượng tam giác ABC vuông tại A, đường cao AH
\(AH^2=BH\cdot HC=9\cdot5=45\\ \Rightarrow AH=3\sqrt{5}\left(cm\right)\)
Đúng 3
Bình luận (0)
Áp dụng hệ thức lượng tam giác ABC vuông tại A, đường cao AH
AH^2=BH⋅HC=9⋅5=45⇒AH=3√5(cm)
Đúng 4
Bình luận (0)
Cho tam giác ABC vuông tại A, biết , BC = 10 cm .
a)Giải tam giác vuông ABC ?
b)Vẽ đường cao AH, đường trung tuyến AM . Tính độ dài AH, HM?
a, \(\tan B=\dfrac{4}{3}\Leftrightarrow\dfrac{AC}{AB}=\dfrac{4}{3}\Leftrightarrow AC=\dfrac{4}{3}AB\)
Áp dụng PTG: \(AB^2+AC^2=AB^2+\dfrac{16}{9}AB^2=\dfrac{25}{9}AB^2=BC^2=100\)
\(\Leftrightarrow AB^2=36\Leftrightarrow AB=6\left(cm\right)\\ \Leftrightarrow AC=6\cdot\dfrac{4}{3}=8\left(cm\right)\)
\(\tan B=\dfrac{4}{3}\approx\tan53^0\Leftrightarrow\widehat{B}\approx53^0\\ \widehat{C}=90^0-\widehat{B}\approx90^0-53^0=37^0\)
b, Vì AM là trung tuyến ứng ch BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{48}{10}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
C1 Cho tam giác vuông ABC vuông tại A, đường cao AH , biết AB9cm,AC12cm, tính độ dài cạnh AH
C2 Cho tam giác ABC vuông tại A, đường cao AH, biết BH5cm,HC6cm. Tính độ dài cạnh AB
C3 Đồ thị hai hàm số y3x + 2 và y (2m+1)x+k-1 là 2 đường thẳng cắt nhau tại 1 điểm trên trục tung khi ( giải hẳn ra)
C4 Trong các hàm số y 3 - 2x ,y √3(x+1)-5;y1/2x+6;y-1,5x hàm số không phải hàm số bậc nhất là (giải hẳn ra)
Giúp mình với
Đọc tiếp
C1 Cho tam giác vuông ABC vuông tại A, đường cao AH , biết AB=9cm,AC=12cm, tính độ dài cạnh AH
C2 Cho tam giác ABC vuông tại A, đường cao AH, biết BH=5cm,HC=6cm. Tính độ dài cạnh AB
C3 Đồ thị hai hàm số y=3x + 2 và y= (2m+1)x+k-1 là 2 đường thẳng cắt nhau tại 1 điểm trên trục tung khi ( giải hẳn ra)
C4 Trong các hàm số y = 3 - 2x ,y =√3(x+1)-5;y=1/2x+6;y=-1,5x hàm số không phải hàm số bậc nhất là (giải hẳn ra)
Giúp mình với
Câu 1:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{9^2}+\dfrac{1}{12^2}=\dfrac{1}{81}+\dfrac{1}{144}=\dfrac{25}{1296}\)
\(\Leftrightarrow AH^2=\dfrac{1296}{25}\)
hay \(AH=\dfrac{14}{5}=4.8cm\)
Vậy: AH=4,8cm
Câu 2:
Ta có: BC=BH+CH(H nằm giữa B và C)
hay BC=5+6=11(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=5\cdot11=55\)
hay \(AB=\sqrt{55}cm\)
Vậy: \(AB=\sqrt{55}cm\)
Câu 4:
Không có hàm số nào không phải là hàm số bậc nhất
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH=4cm, CH=9cm. Độ dài đường cao AH là?
Theo HTL:
AH2 = HB . HC
= 4 . 9
= 36
AH = 6 cm
Đúng 0
Bình luận (0)