B1 : Cho A= abc ; B=a^3b;C= c^5
CMR A,B,C ko thể cùng âm
B2 : Tìm số nguyên dương n sao cho n+2 là ước của 111 còn n-2 là bội của 11
Cho tam giác ABC có hai đường cao A,A1 . B,B1 . CMR A1B1C ĐỒNG DẠNG ABC
Sửa đề: Đường chéo AE,BD
Xét ΔAEC vuông tại E và ΔBDC vuông tại D có
góc C chung
Do đó: ΔAEC\(\sim\)ΔBDC
=>AC/BC=AE/BD=CE/CD
hay AC/CE=BC/CD
Xét ΔABC và ΔCED có
AC/CD=BC/CD
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔCED
B1:Cho tam giác ABC biết A-B=B-C=10 độ. Tính các hóc của tam giác ABC.
Ta có: \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}=10^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=2\widehat{B}\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=2\widehat{B}+\widehat{B}\)
\(\Rightarrow3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}=10^0+\widehat{B}=70^0\\\widehat{C}=\widehat{B}-10^0=50^0\end{matrix}\right.\)
Cho hình chóp S.ABCD có đáy ABC là tam giác với AB=2cm,AC=3cm, B A C ^ = 60 0 . S A ⊥ ( A B C ) . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối cầu đi qua năm điểm A,B,C, B 1 , C 1
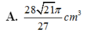
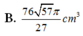
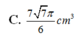
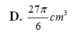
Cho hình chóp S.ABCD có đáy ABC là tam giác với AB=2 cm, AC=3cm, ∠ B A C = 60 ° , S A ⊥ ( A B C ) . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối cầu đi qua năm điểm A, B, C, B 1 , C 1
A. 28 21 π 27 c m 3
B. 76 57 π 27 c m 3
C. 7 7 π 6 c m 3
D. 27 π 6 c m 3
Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
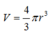
Cách giải:
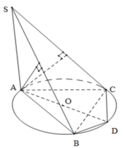
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D

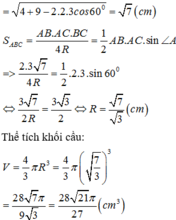
Cho hình chóp S.ABC có ABC là tam giác mà A B = 1 , A C = 2 , B A C ^ = 60 ∘ ; SA vuông góc với mặt phẳng (ABC). Gọi B 1 , C 1 là hình chiếu của A lên SB, SC. Tính diện tích mặt cầu đi qua bốn đỉnh A , B , C , B 1 , C 1 ?
A. 8 π
B. 4 π
C. 16 π
D. 12 π
B1. Cho ABC vuông tại A đường cao AH, AB=9cm, AC=12cm
a. Tính DC, AH
b. Chứng minh ABC đồng dạng với HBA
a: BC=15cm
\(AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
B1 :Tìm số thích hợp thay cho các chữ số dưới đây
a) ad+bc+ca=abc
b)abcd+abc+ab+a=4321
a)ad + bc + ca = abc
<=> 100a + bc = 10a + b + 10c + a + bc
<=> 100a = ab + ca
<=> 100a = 11a + b + 10c
<=> 89a = cb
=>abc = 198
b)
Ký hiệu (abcd) là số tự nhiên có 4 chữ số.
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d
Vậy 1111.a + 111.b + 11.c + d = 4321
+ Nếu a < 3 => 111.b + 11.c + d > 2098 (không được vì b, c, d < 10)
+ Nếu a > 3 => vế trái > 4321
Vậy a = 3 => 111.b + 11.c + d = 988
+ Nếu b < 8 => 11.c + d > 210 (không được vì c, d < 10)
+ Nếu b > 8 => vế trái > 988
Vậy b = 8 => 11.c + d = 100
+ Nếu c < 9 => d > 11 (không được)
Vậy c = 9; d = 1
=> (abcd) = 3891
các chữ thay số đều có dấu gạch trên đầu
hong biết lm , mún mk biết lm thì phải tk mk
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A,B,C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Đáp án B.
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ I A = I B = I C (1).
Ta có ∆ S A C = ∆ S A B ⇒ A B 1 = A C 1 . Từ đây ta chứng minh được B 1 C 1 / / B C .
Gọi M là trung điểm của B C ⇒ B C ⊥ S A M ⇒ B 1 C 1 ⊥ S A M .
Gọi H = S M ∩ B 1 C 1 ⇒ H B 1 M B = H C 1 M C , do M B = M C nên H B 1 = H C 1
Mặt phẳng (SAM) đi qua trung điểm H của B 1 C 1 nên B 1 C 1 ⊥ S A M nên (SAM) là mặt phẳng trung trực của B 1 C 1 . Do I ∈ A M ⊂ S A M nên I B 1 = I C 1 (2).
Gọi N là trung điểm của AB, suy ra A B ⊥ I N S A ⊥ I N ⇒ I N ⊥ S A B .
Tam giác A B B 1 vuông tại B 1 có N là trung điểm của AB nên N A = N B 1 = 1 2 A B .
Như vậy ta có các tam giác vuông sau bằng nhau
∆ I N A = ∆ I N B = ∆ I N B 1 ⇒ I A = I B = I B 1 (3).
Từ (1), (2) và (3) suy ra 5 điểm A,B,C, B 1 , C 1 cùng nằm trên mặt cầu tâm I, bán kính R = I A = 2 3 . a 3 2 = a 3 3 (do ABC là tam giác đều và I là tâm đường tròn ngoại tiếp ⇒ I cũng là trọng tâm tam giác ABC).
Cho tam giác ABC có A 2 ; 3 , B 1 ; − 2 , C 6 ; 2 . Phép tịnh tiến T BC → biến tam giác ABC thành tam giác A′B′C′. Tọa độ trọng tâm tam giác A′B′C′ là
A. − 2 ; − 3
B. 2 ; 3
C. 8 ; 5
D. 3 ; 1