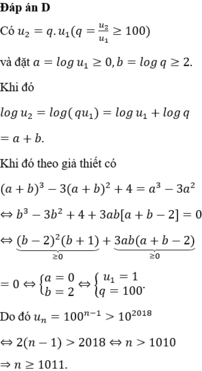A=102017/102018+1 ; B=102018/102019+1 so sánh a và b

Những câu hỏi liên quan
so sánh A và B
a, A= 102017 +1/ 102018+1 , B =102018 +1/ 102019+1
\(A=\dfrac{10^{2017}+1}{10^{2018}+1}\)
=>\(10A=\dfrac{10^{2018}+1+9}{10^{2018}+1}=1+\dfrac{9}{10^{2018}+1}\)
\(B=\dfrac{10^{2018}+1}{10^{2019}+1}\)
=>\(10B=\dfrac{10^{2019}+1+9}{10^{2019}+1}=1+\dfrac{9}{10^{2019}+1}\)
Do đó:\(10B< 10A\)=>\(B< A\)
Đúng 0
Bình luận (1)
\(A=\dfrac{10^{2017}+1}{10^{2018}+1}\)
\(10A=\dfrac{10\left(10^{2017}+1\right)}{10^{2018}+1}=\dfrac{10^{2018}+10}{10^{2018}+1}=\dfrac{10^{2018}+1+9}{10^{2018}+1}=\dfrac{10^{2018}+1}{10^{2018}+1}+\dfrac{9}{10^{2018}+1}=1+\dfrac{9}{10^{2018}+1}\)\(B=\dfrac{10^{2018}+1}{10^{2019}+1}\)
\(10B=\dfrac{10\left(10^{2018}+1\right)}{10^{2019}+1}=\dfrac{10^{2019}+10}{10^{2019}+1}=\dfrac{10^{2019}+1+9}{10^{2019}+1}=\dfrac{10^{2019}+1}{10^{2019}+1}+\dfrac{9}{10^{2019}+1}=1+\dfrac{9}{10^{2019}+1}\)Vì \(1+\dfrac{9}{10^{2018}+1}>1+\dfrac{9}{10^{2019}+1}\)
Nên \(10A>10B\)
Nên \(A>B\)
Đúng 0
Bình luận (0)
Cho cấp số nhân
(
u
n
)
thoả mãn
u
2
≥
100
u
1
≥
1
. Đặt
f
(
x
)
x
3
-
3
x
2
. Biết
f
(
l
o
g
u
2
)...
Đọc tiếp
Cho cấp số nhân ( u n ) thoả mãn u 2 ≥ 100 u 1 ≥ 1 . Đặt f ( x ) = x 3 - 3 x 2 . Biết f ( l o g u 2 ) + 4 = f ( l o g u 1 ) . Tìm số tự nhiên n nhỏ nhất sao cho u n > 10 2018 .
A. 1010.
B. 2020.
C. 2019.
D. 1011.
B ài 1
So sánh M=102018+1 phần 10 mu 2019+1
N=102020+1 phân 10 mu 2021+1
Bài 2
Tim nEN để n phần n + 1 + 2 phần n+1 là số tự nhiên
Bài 3
a) 3 phần 9 - 2 phần 5
b) 4 phần 7 - 3 phần 5
Bài 4
a) x phần 3 + x phần 4 = 21 phan-12
b) x-3 phần -2 = -8 phân x - 3
a^7-a=a(a^6-1)
=a(a^3+1)(a^3-1)
=a(a+1)(a^2-a+1)(a-1)(a^2+a+1)
=a(a-1)(a+1)(a^2-a+1)(a^2+a+1)
*=a(a-1) (a+1) (a^2-a+1-7) (a^2+a+1)
+7a (a-1) (a+1) (a^2+a-1)
*=a (a-1) (a+1) (a^2-a-6) (a^2+a+1-7)
+7a (a-1) (a+1) (a^2+a-1)
+7a (a-1) (a+1) (a^2-a-6)
có: 7a(a-1) (a+1) (a^2+a-1)+7a (a-1) (a+1) (a^2-a-6) chia hết cho 7
Giải thích giùm mình phần * đc k ạ.
the exam is very difficult ......... Help help help ..............thanks
1*1*11*1*1*11*1*1*1*1*11*1*1*1*1*1*1*11*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a*a-500=200
(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) với a -1 , b 25(a^2 +b^2 -1)-(a.b^2-a) v...
Đọc tiếp
(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25^2 -1)(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25-(a.b^2-a) với a= -1 , b=(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25 25(a^2 +b^2 -1)-(a.b^2(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25-a) với a= -1 (a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25(a^2 +b^2 -1)-(a.b^2-a) với a= -1 , b= 25=5 25
một câu hỏi rất đáng khen ,.. very good!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
A=a√a-1/a-√a-a√a+1/a+√a+(√a-1/√a) (√a+1/√a-1+√a-1/√a+1)
CMR:
a) 1/a(a+1)=a/1-1/a+1
b)2/a(a+1)(a+2)=1/a(a+1)-1/(a+1)(a+2)
a, đề phải là 1/a.(a+1) = 1/a - 1/a+1 chứ bạn !
Có : 1/a.(a+1) = (a+1)-a/a.(a+1) = a+1/a.(a+1) - a/a.(a+1) = 1/a - 1/a+1
=> 1/a.(a+1) = 1/a - 1/a+1
b, Có : 2/a.(a+1).(a+2) = (a+2)-a/a.(a+1).(a+2) = a+2/a.(a+1).(a+2) - a/a.(a+1).(a+2) = 1/a.(a+1) - 1/(a+1).(a+2)
=> 2/a.(a+1).(a+2) = 1/a.(a+1) - 1/(a+1).(a+2)
Tk mk nha
Đúng 0
Bình luận (0)
a, \(VP=\frac{1}{a}-\frac{1}{a+1}=\frac{a+1}{a\left(a+1\right)}-\frac{a}{a\left(a+1\right)}==\frac{a+1-a}{a\left(a+1\right)}=\frac{1}{a\left(a+1\right)}=VT\)
b, \(VP=\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}=\frac{a+2}{a\left(a+1\right)\left(a+2\right)}-\frac{a}{a\left(a+1\right)\left(a+2\right)}=\frac{a+2-a}{a\left(a+1\right)\left(a+2\right)}=\frac{2}{a\left(a+1\right)\left(a+2\right)}=VT\)
Đúng 0
Bình luận (0)
Bài 1: Cho biểu thức:
B= \(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\)+(\(1-\dfrac{1}{\sqrt{a}}\)) (\(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt[]{a}-1}{\sqrt{a}+1}\))
Rút gọn B
\(B=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{\sqrt{a}-1}{\sqrt{a}}\cdot\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
\(=2+\dfrac{1}{\sqrt{a}}\cdot\dfrac{2a+2}{\sqrt{a}+1}\)
\(=\dfrac{2a+2\sqrt{a}+2a+2}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{4a+2\sqrt{a}+2}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
Đúng 5
Bình luận (0)
a) \(\dfrac{a-1}{\sqrt{b}-1}\).\(\sqrt{\dfrac{b-2\sqrt{b}+1}{\left(a-1\right).4}}\) (a,b≠1,b>0)
b) (1+\(\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\)).(1-\(\dfrac{a-\sqrt{a}}{\sqrt{a-1}}\)) (a≠1,a>0)
a) Ta có: \(\dfrac{a-1}{\sqrt{b}-1}\cdot\sqrt{\dfrac{b-2\sqrt{b}+1}{\left(a-1\right)\cdot4}}\)
\(=\dfrac{a-1}{\sqrt{b}-1}\cdot\dfrac{\sqrt{b}-1}{2\sqrt{a-1}}\)
\(=\dfrac{\sqrt{a-1}}{2}\)
b) Ta có: \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=1-a\)
Đúng 1
Bình luận (0)