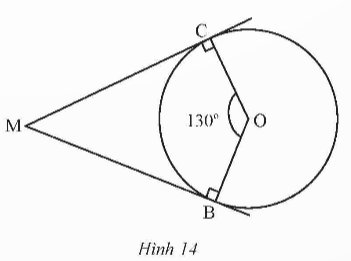
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .
Những câu hỏi liên quan
Cho đường tròn (O; 3cm) và điểm M nằm ngoài đường tròn sao cho OM 5cm. Kẻ tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm ). Từ B kẻ đường thẳng vuông góc MO tại N cắt đường tròn (O) tại C.a) CM: MC là tiếp tuyến của đường tròn (O).b) Tính độ dài MN và NO.c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chu vi tam giác MED.d) Tính diện tích tứ giác MBOC.
Đọc tiếp
Cho đường tròn (O; 3cm) và điểm M nằm ngoài đường tròn sao cho OM = 5cm. Kẻ tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm ). Từ B kẻ đường thẳng vuông góc MO tại N cắt đường tròn (O) tại C.
a) CM: MC là tiếp tuyến của đường tròn (O).
b) Tính độ dài MN và NO.
c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chu vi tam giác MED.
d) Tính diện tích tứ giác MBOC.
28 tháng 12 2023 lúc 8:24
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
28 tháng 12 2023 lúc 10:45
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
28 tháng 12 2023 lúc 13:36
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giúp mik vs ah , mik đang cần gấppppp
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giúp mik vs ah , mik đang cần gấppppp
b: Xét (O) có
ΔCAB nội tiếp
CB là đường kính
Do đó: ΔCAB vuông tại A
=>CA\(\perp\)AB tại A
=>CA\(\perp\)BE tại A
Ta có: \(\widehat{OAE}=\widehat{OAC}+\widehat{EAC}=\widehat{OAC}+90^0\)
\(\widehat{MAC}=\widehat{MAO}+\widehat{OAC}=\widehat{OAC}+90^0\)
Do đó: \(\widehat{OAE}=\widehat{MAC}\)
Xét tứ giác CKAE có \(\widehat{CKE}=\widehat{CAE}=90^0\)
nên CKAE là tứ giác nội tiếp
=>\(\widehat{ACK}=\widehat{AEK}\)
=>\(\widehat{ACM}=\widehat{AEO}\)
Xét ΔAMC và ΔAOE có
\(\widehat{ACM}=\widehat{AEO}\)
\(\widehat{MAC}=\widehat{OAE}\)
Do đó: ΔAMC đồng dạng với ΔAOE
=>\(\dfrac{AM}{AO}=\dfrac{AC}{AE}\)
=>\(AM\cdot AE=AO\cdot AC\)
Đúng 0
Bình luận (0)
28 tháng 12 2023 lúc 13:11
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giúp mik vs ah , mik đang cần gấppppp
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giúp mik vs ah , mik đang cần gấppppp
28 tháng 12 2023 lúc 15:50
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé 1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là h...
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
28 tháng 12 2023 lúc 16:59
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
a: Ta có: ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(MA^2=15^2-9^2=144\)
=>\(MA=\sqrt{144}=12\left(cm\right)\)
Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{3}{5}\)
nên \(\widehat{AMO}\simeq36^052'\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}\simeq73^044'\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=OC^2\)
Xét ΔOHE vuông tại H và ΔOKM vuông tại K có
\(\widehat{HOE}\) chung
Do đó: ΔOHE đồng dạng với ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{OE}{OM}\)
=>\(OK\cdot OE=OH\cdot OM\)
=>\(OK\cdot OE=OC^2\)
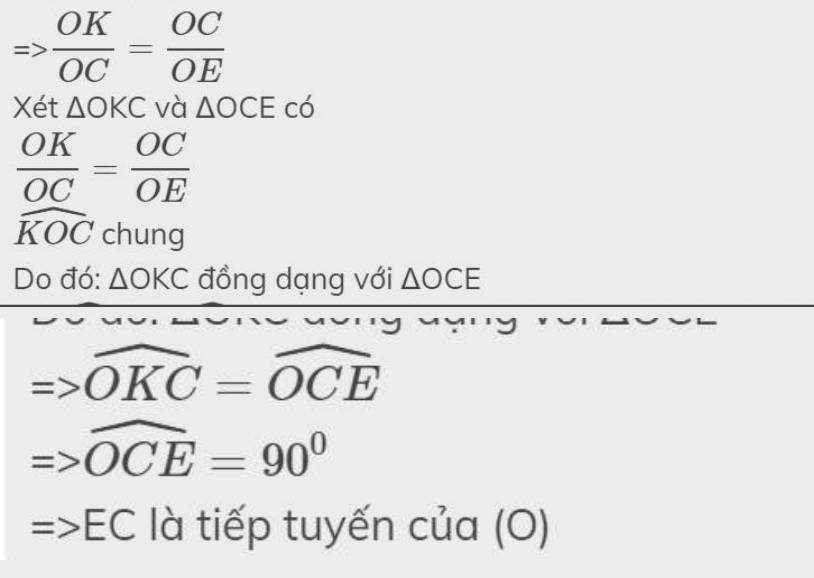
=>\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
Xét ΔOKC và ΔOCE có
\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
\(\widehat{KOC}\) chung
Do đó: ΔOKC đồng dạng với ΔOCE
=>\(\widehat{OKC}=\widehat{OCE}\)
=>\(\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại C (CA CB) và nội tiếp đường tròn (O). Gọi Ilà hình chiếu của O trên AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O) ở M.a) Chứng minh rằng MC là tiếp tuyến của đường tròn tâm (O).b) Đường thẳng MB cắt đường tròn (O) tại N khác B. Chứng minh rằng tứ giác NIOB nội tiếp.c) Lấy điểm P sao cho N là trung điểm AP. Gọi H là hình chiếu của P trên đường thẳng AM.Chứng minh rằng đường thẳng BC đi qua trung điểm đoạn PH.Mình đang gấp nên các bn giúp mình nhanh với
Đọc tiếp
Cho tam giác ABC vuông tại C (CA > CB) và nội tiếp đường tròn (O). Gọi I
là hình chiếu của O trên AC. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn (O) ở M.
a) Chứng minh rằng MC là tiếp tuyến của đường tròn tâm (O).
b) Đường thẳng MB cắt đường tròn (O) tại N khác B. Chứng minh rằng tứ giác NIOB nội tiếp.
c) Lấy điểm P sao cho N là trung điểm AP. Gọi H là hình chiếu của P trên đường thẳng AM.
Chứng minh rằng đường thẳng BC đi qua trung điểm đoạn PH.
Mình đang gấp nên các bn giúp mình nhanh với
a: ΔOAC cân tại O có OI là đường cao
nên OI là phân giác của góc AOC
Xét ΔOAM và ΔOCM có
OA=OC
góc AOM=góc COM
OM chung
=>ΔOAM=ΔOCM
=>góc OCM=90 độ
=>MC là tiếp tuyến của (O)
b: góc ANB=1/2*sđ cung AB=90 độ
=>AN vuông góc MB
ΔMAB vuông tại A có AN là đường cao
nên MA^2=MN*MB
ΔMAO vuông tại A có AI là đường cao
nên MI*MO=MA^2
=>MN*MB=MI*MO
=>MN/MO=MI/MB
=>ΔMNI đồng dạng với ΔMOB
=>góc MNI=góc MOB
=>góc INB+góc IOB=180 độ
=>INBO nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác MBC cân tại M, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc M. O là trung điểm IK.
a, B, I, C, K cùng thuộc (O)
b, MC là tiếp tuyến của(O)
c, Bán kính đường tròn (O)=?, biết MB=MC=10
BC=12
Từ điểm M nằm ngoài đường tròn vẽ tiếp tuyến MA tới đường tròn (O; R), ( A là tiếp điểm). Gọi E là trung điểm đoạn AM và hai điểm I, H lần lượt là hình chiếu của E và A trên đường thẳng OM. Qua M vẽ cát tuyến MBC tới đường tròn (O) sao cho MB MC và tia MC nằm giữa hai tia MA, MO.a) Chứng minh . góc AHB góc AHCb) Vẽ tiếp tuyến IK tới đường tròn (O) với K là tiếp điểm. Chứng minh . ∆MKH vuông tại K.
Đọc tiếp
Từ điểm M nằm ngoài đường tròn vẽ tiếp tuyến MA tới đường tròn (O; R), ( A là tiếp điểm). Gọi E là trung điểm đoạn AM và hai điểm I, H lần lượt là hình chiếu của E và A trên đường thẳng OM. Qua M vẽ cát tuyến MBC tới đường tròn (O) sao cho MB < MC và tia MC nằm giữa hai tia MA, MO.
a) Chứng minh . góc AHB = góc AHC
b) Vẽ tiếp tuyến IK tới đường tròn (O) với K là tiếp điểm. Chứng minh . ∆MKH vuông tại K.