a,Rút gọn phân thức;
\(\frac{15xy^2\left(x-y\right)}{25xy\left(y-x\right)}\)
b, CMR: A=\(x^2-x+1>0,\forall x\in R\)
a) Thay phân thức P = uv u − v vào biểu thức A = uP u + P − vP v − P rồi rút gọn;
b) Thay hai phân thức P = 2 mn m 2 + n 2 và Q = 2 mn m 2 + n 2 vào biểu thức B = P 2 Q 2 P 2 − Q 2 rồi rút gọn;
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
Nêu qui tắc rút gọn một phân thức đại số. Hãy rút gọn phân thức
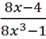
Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn:
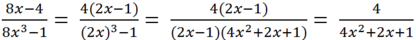
Rút gọn phân thức (a + b) 2 − c 2 a + b + c ta được phân thức có tử là?
A. a - b - c
B. a +b + c
C. a - b + c
D. a + b - c
\(A=\dfrac{x^2-2x+1}{x^2-1}\)
a) tìm điều kiên xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=3
BÀI5
\(B=\dfrac{6x-2y}{9x^2-y^2}\)
a)tìm điều kiện xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=1 y=-1/2
a) ĐKXĐ:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
b) \(A=\dfrac{x^2-2x+1}{x^2-1}\)
\(A=\dfrac{x^2-2\cdot x\cdot1+1^2}{x^2-1^2}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(A=\dfrac{x-1}{x+1}\)
c) Thay x = 3 vào A ta có:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
a) ĐKXĐ:
\(9x^2-y^2\ne0\Leftrightarrow\left(3x\right)^2-y^2\ne0\Leftrightarrow\left(3x-y\right)\left(3x+y\right)\ne0\)
\(\Leftrightarrow3x\ne\pm y\)
b) \(B=\dfrac{6x-2y}{9x^2-y^2}\)
\(B=\dfrac{2\cdot3x-2y}{\left(3x\right)^2-y^2}\)
\(B=\dfrac{2\left(3x-y\right)}{\left(3x+y\right)\left(3x-y\right)}\)
\(B=\dfrac{2}{3x+y}\)
Thay x = 1 và \(y=\dfrac{1}{2}\) và B ta có:
\(B=\dfrac{2}{3\cdot1+\dfrac{1}{2}}=\dfrac{2}{3+\dfrac{1}{2}}=\dfrac{2}{\dfrac{7}{2}}=\dfrac{4}{7}\)
RÚT GỌN
\(P=\frac{2x^2-8}{x-2}\)
a) rút gọn phân thức P
b) tìm giá trị của x để giá trị của phân thức P =2
\(P=\frac{2x^2-8}{x-2}=\frac{2.\left(x^2-2^2\right)}{x-2}=\frac{2.\left(x-2\right).\left(x+2\right)}{x-2}=2x+4\left(x\ne2\right)\)
\(P=2x+4=2\Rightarrow2x=-2\Rightarrow x=-1\)
bài 1 rút gọn biểu thức
(x-2)^2-(x-3^2)
bài 2
cho phân thưc p =1-4x^2/4x^2-4x+1
a) rút gọn phân thức
b) tính giá trị của phân thức tại x=-4
Bài 1 :
\(\left(x-2\right)^2-\left(x-3^2\right)=\left(x-2\right)^2-\left(x-9\right)\)
\(=x^2-4x+4-x+9=x^2-5x+13\)
Bài 2 :
a, \(P=\frac{1-4x^2}{4x^2-4x+1}=\frac{\left(1-2x\right)\left(2x+1\right)}{\left(2x-1\right)^2}\)
\(=\frac{-\left(2x-1\right)\left(2x+1\right)}{\left(2x-1\right)^2}=\frac{-\left(2x+1\right)}{2x-1}=\frac{-2x-1}{2x-1}\)
b, Thay x = -4 ta được :
\(\frac{-2.\left(-4\right)-1}{2.\left(-4\right)-1}=\frac{8-1}{-8-1}=-\frac{7}{9}\)
Cho phân thức \(\dfrac{x^2-10x+25}{x^2-5x}\)
a. Tìm điều kiện xác định của phân thức
b. Rút gọn phân thức
a. \(x^2-5x\ne0\)
=> ĐKXĐ: \(x\left(x-5\right)\ne0\) => \(\left\{{}\begin{matrix}x\ne0\\x\ne5\end{matrix}\right.\)
b. \(\dfrac{x^2-10x+25}{x^2-5x}\)
= \(\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}\)
= \(\dfrac{x-5}{x}\)
Cho phân thức A = x 2 - 6 x + 9 x 2 - 9
b) Rút gọn A
rút gọn phân thức A=x^2+2x-3/x+3
\(A=\dfrac{x^2+2x-3}{x+3}=\dfrac{x^2+3x-x-3}{x+3}=\dfrac{\left(x+3\right)\left(x-1\right)}{x+3}=x-1\)
\(A=\dfrac{x^2+2x-3}{x+3}=\dfrac{x^2-x+3x-3}{x+3}=\dfrac{x\left(x-1\right)+3\left(x-1\right)}{x+3}=\dfrac{\left(x-1\right)\left(x+3\right)}{x+3}=x-1\)
Rút Gọn Phân Thức: (a+b)^3 +(a-b)^3 -2a^3
\(\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
=\(a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
=\(\left(a^3+a^3\right)+\left(3a^2b-3a^2b\right)+\left(3ab^2+3ab^2\right)+\left(b^3-b^3\right)-2a^3\)
=\(2a^3+9ab^2-2a^3\)
=\(9ab^2\)