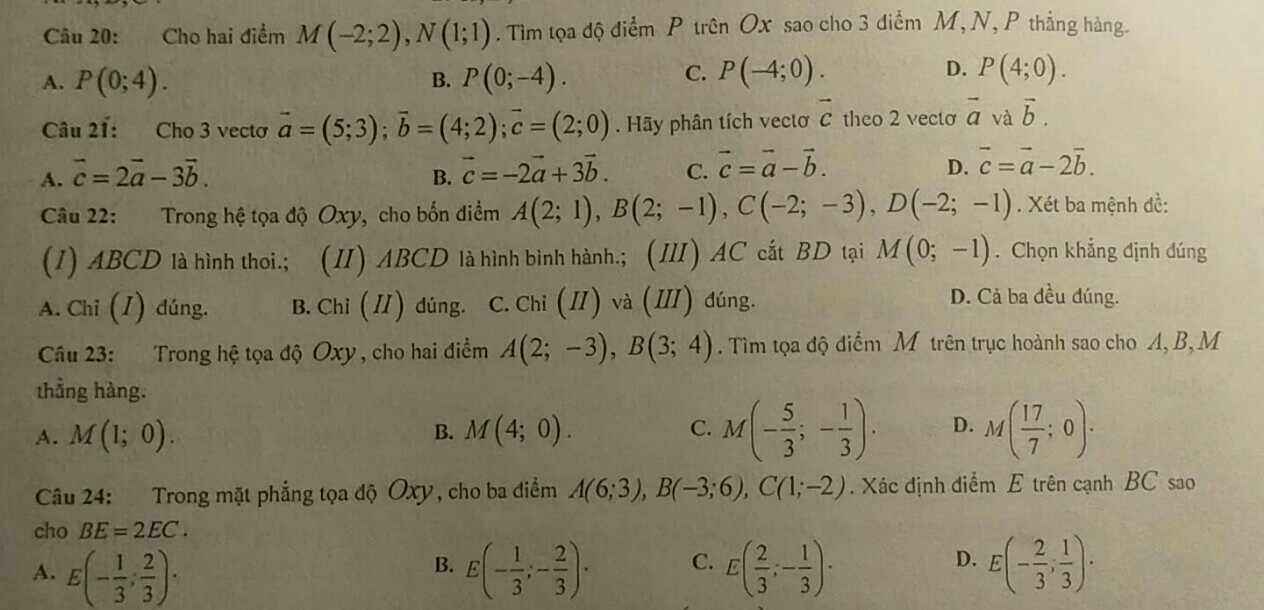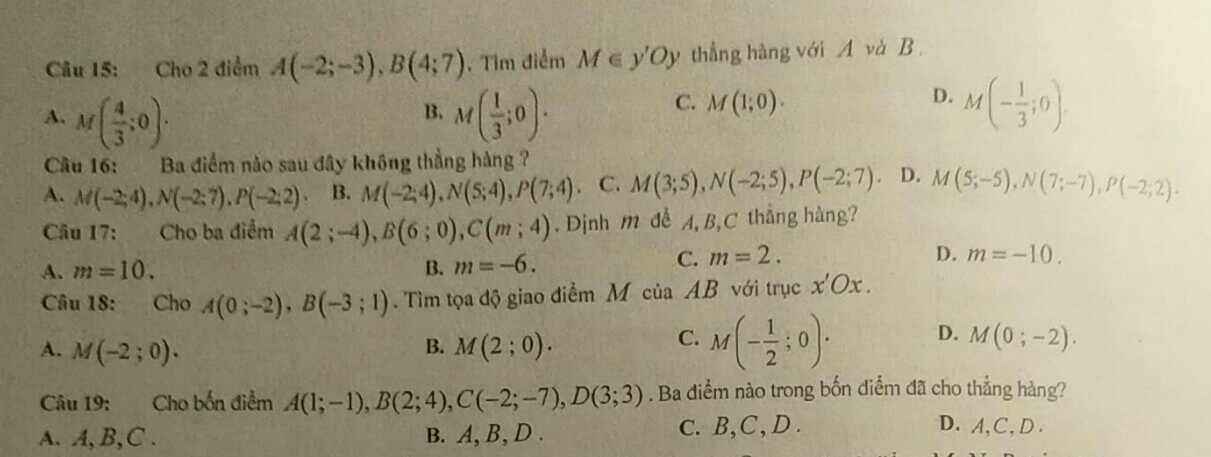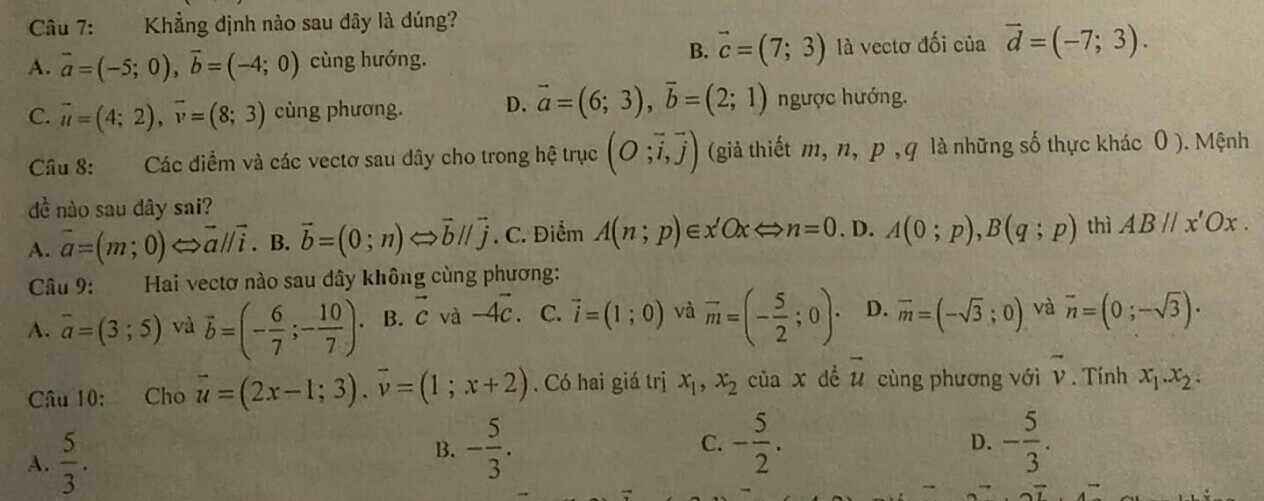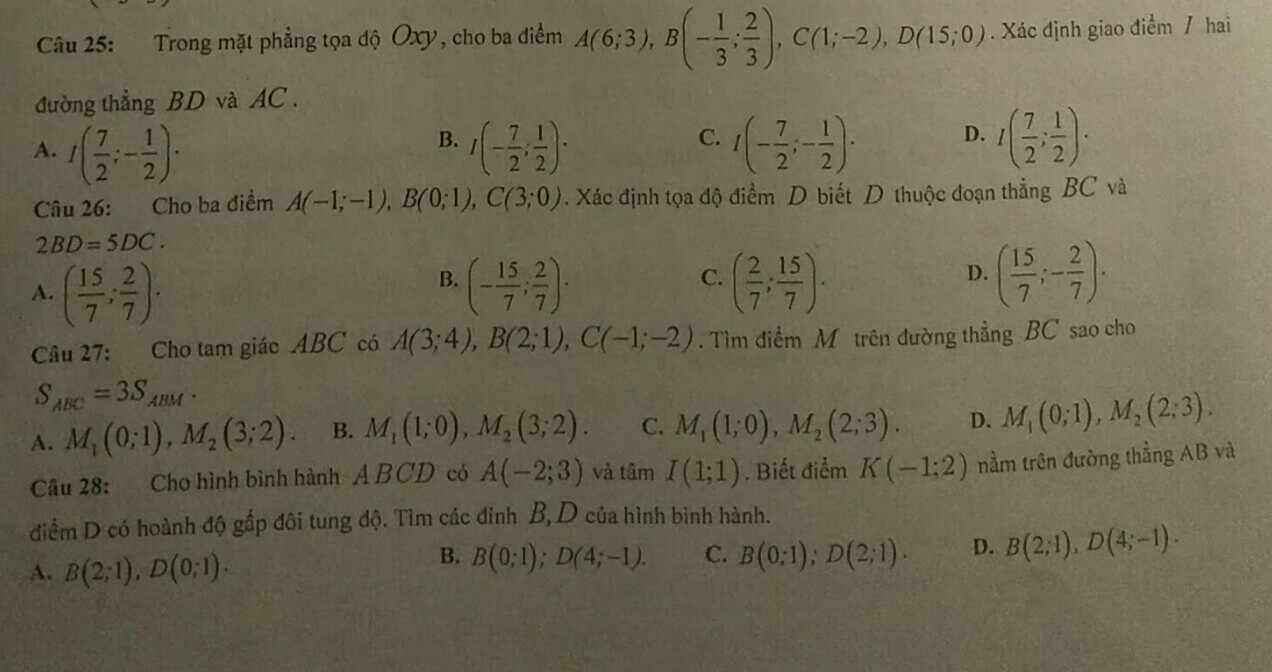
Câu 25 :
\(\overrightarrow{AC}=\left(-5;-5\right)\Rightarrow\overrightarrow{n_p}=\left(5;-5\right)=5\left(1;-1\right)\)
\(\left(AC\right):\left(x-1\right)-\left(y+2\right)=0\)
\(\Rightarrow\left(AC\right):x-y-3=0\)
\(\overrightarrow{BD}=\left(\dfrac{46}{3};-\dfrac{2}{3}\right)\Rightarrow\overrightarrow{n_p}=\left(\dfrac{2}{3};\dfrac{46}{3}\right)=\dfrac{2}{3}\left(1;23\right)\)
\(\left(BD\right):\left(x-15\right)+23\left(y-0\right)=0\)
\(\Rightarrow\left(BD\right):x+23y-15=0\)
\(I\left(x;y\right)=\left(BD\right)\cap\left(AC\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-y-3=0\\x+23y-15=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{7}{2};\dfrac{1}{2}\right)\Rightarrow\) Chọn D
Câu 26 :
\(2BD=5DC\Rightarrow\dfrac{BD}{DC}=\dfrac{5}{2}\)
\(\Rightarrow D\) chia \(BC\) theo tỉ lệ \(5:2\), với \(B\) là đầu mút gần hơn
Gọi \(D\left(x_D;y_D\right)\Rightarrow\left\{{}\begin{matrix}x_D=\dfrac{5.x_C+2.x_B}{5+2}=\dfrac{5.3+2.0}{7}=\dfrac{15}{7}\\y_D=\dfrac{5.y_C+2.y_B}{5+2}=\dfrac{5.0+2.1}{7}=\dfrac{2}{7}\end{matrix}\right.\)
\(\Rightarrow I\left(\dfrac{15}{7};\dfrac{2}{7}\right)\Rightarrow\) Chọn A
Đúng 0
Bình luận (0)
Câu 20 : \(P\in\left(Ox\right)\Rightarrow P\left(x;0\right)\)
\(\overrightarrow{MN}=\left(3;-1\right)\)
\(\overrightarrow{MP}=\left(x+2;-2\right)\)
\(M,N,P\) thẳng hàng khi \(\overrightarrow{MN};\overrightarrow{MP}\) cùng phương
\(\Rightarrow\dfrac{x+2}{3}=\dfrac{-2}{-1}\Rightarrow x=4\)
\(\Rightarrow P\left(4;0\right)\Rightarrow\) Chọn D
Câu 21 :
\(\overrightarrow{c}=x.\overrightarrow{a}+y.\overrightarrow{b}\)
\(\Rightarrow\left(2;0\right)=x\left(5;3\right)+y\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}5x+4y=2\\3x+2y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\) \(\Rightarrow\overrightarrow{c}=-2\overrightarrow{a}+3\overrightarrow{b}\Rightarrow\) Chọn B
Câu 22
\(\overrightarrow{AB}=\left(0;-2\right)\overrightarrow{CD}=\left(0;2\right)\Rightarrow\overrightarrow{AB}=-\overrightarrow{CD}\left(1\right)\)
\(\)\(\overrightarrow{AD}=\left(-4;-2\right)\overrightarrow{BC}=\left(-4;-2\right)\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow ABCD\) là hình bình hành (Đúng) (II)
\(\overrightarrow{AC}=\left(-4;-4\right)\Rightarrow\overrightarrow{n_p}=\left(4;-4\right)=4\left(1;-1\right)\)
\(\Rightarrow\left(AC\right):\left(x-2\right)-\left(y-1\right)=0\Rightarrow x-y-1=0\)
\(\overrightarrow{BD}=\left(-4;0\right)\Rightarrow\overrightarrow{n_p}=\left(0;-4\right)=\left(0;-1\right)\)
\(\Rightarrow\left(BD\right):-\left(y+1\right)=0\Rightarrow y=-1\)
Ta thấy \(M\left(0;-1\right)=\left(AC\right)\cap\left(BD\right)\left(Đúng\right)\) (III)
Vậy \(\left(II\right)\&\left(III\right)\) đúng \(\Rightarrow\) Chọn C
Đúng 0
Bình luận (0)
Câu 15: M thuộc trục Oy nên M(0;y)
A(-2;-3); B(4;7); M(0;y)
\(\overrightarrow{AB}=\left(4+2;7+3\right)=\left(6;10\right)\)
\(\overrightarrow{AM}=\left(0+2;y+3\right)=\left(2;y+3\right)\)
Để A,B,M thẳng hàng thì \(\dfrac{y+3}{10}=\dfrac{2}{6}=\dfrac{1}{3}\)
=>\(y+3=\dfrac{10}{3}\)
=>\(y=\dfrac{1}{3}\)
=>\(M\left(0;\dfrac{1}{3}\right)\)
Câu 17: A(2;-4); B(6;0); C(m;4)
\(\overrightarrow{AB}=\left(6-2;0+4\right)\)
=>\(\overrightarrow{AB}=\left(4;4\right)\)
\(\overrightarrow{AC}=\left(m-2;4+4\right)\)
=>\(\overrightarrow{AC}=\left(m-2;8\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{m-2}{4}=\dfrac{8}{4}\)
=>m-2=8
=>m=10
=>Chọn A
Câu 18: M thuộc trục x'Ox nên M(x;0)
A(0;-2); B(-3;1); M(x;0)
\(\overrightarrow{AB}=\left(-3-0;1+2\right)=\left(-3;3\right)=\left(-1;1\right)\)
\(\overrightarrow{AM}=\left(x-0;0+2\right)=\left(x;2\right)\)
A,B,M thẳng hàng
=>\(\dfrac{x}{-1}=\dfrac{2}{1}=2\)
=>x=-2
=>M(-2;0)
=>Chọn A
Câu 19: A(1;-1); B(2;4); C(-2;-7); D(3;3)
\(\overrightarrow{AB}=\left(2-1;4+1\right)=\left(1;5\right)\)
\(\overrightarrow{AC}=\left(-2-1;-7+1\right)=\left(-3;-6\right)\)
=>\(\overrightarrow{CA}=\left(3;6\right)=\left(1;2\right)\)
\(\overrightarrow{AD}=\left(3-1;3+1\right)=\left(2;6\right)\)
\(\overrightarrow{BC}=\left(-2-2;-7-4\right)=\left(-4;-11\right)\)
\(\overrightarrow{BD}=\left(3-2;3-4\right)=\left(1;1\right)\)
\(\overrightarrow{CD}=\left(3+2;3+7\right)=\left(5;10\right)\)
Vì \(\dfrac{1}{5}=\dfrac{2}{10}\)
nên C,A,D thẳng hàng
=>Chọn D
Đúng 0
Bình luận (0)
Câu 11: \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}+4\overrightarrow{c}\)
=>\(\left\{{}\begin{matrix}x_{\overrightarrow{u}}=3\cdot1+2\cdot\left(-3\right)+4\cdot\left(-4\right)=3-6-16=-19\\y_{\overrightarrow{u}}=3\cdot2+2\cdot1+4\cdot2=16\end{matrix}\right.\)
=>Chọn B
Câu 12: A(2;5); B(1;7); C(1;5); D(0;9)
\(\overrightarrow{AB}=\left(1-2;7-5\right)=\left(-1;2\right)\)
\(\overrightarrow{AC}=\left(1-2;5-5\right)=\left(-1;0\right)\)
\(\overrightarrow{AD}=\left(-2;4\right)\)
Vì \(\dfrac{-1}{-2}=\dfrac{2}{4}\)
nên A,B,D thẳng hàng
=>Chọn D
Câu 13: \(AB=\sqrt{\left(4-3\right)^2+\left(-3-0\right)^2}=\sqrt{10}\)
\(BC=\sqrt{\left(8-4\right)^2+\left(-1+3\right)^2}=2\sqrt{5}\)
\(CD=\sqrt{\left(-2-8\right)^2+\left(1+1\right)^2}=2\sqrt{26}\)
\(AC=\sqrt{\left(8-3\right)^2+\left(-1-0\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)
\(AD=\sqrt{\left(-2-3\right)^2+\left(1-0\right)^2}=\sqrt{26}\)
Vì AC+AD=CD
nên C,A,D thẳng hàng
=>Chọn D
Câu 14:
A(-2m;-m); B(2m;m); O(0;0)
Để đường thẳng AB đi qua O thì A,B,O thẳng hàng
\(\overrightarrow{AB}=\left(4m;2m\right);\overrightarrow{AO}=\left(2m;m\right)\)
Để A,B,O thẳng hàng thì \(\dfrac{4m}{2m}=\dfrac{2m}{m}\)
=>2=2(đúng)
=>Chọn C
Đúng 0
Bình luận (0)
Câu 7: A
Câu 8: C
Câu 9: D
Câu 10: Để \(\overrightarrow{u};\overrightarrow{v}\) là hai vecto cùng phương thì \(\dfrac{2x-1}{1}=\dfrac{3}{x+2}\)
=>(2x-1)(x+2)=3
=>\(2x^2+4x-x-2-3=0\)
=>\(2x^2+3x-5=0\)
=>\(x_1\cdot x_2=\dfrac{c}{a}=-\dfrac{5}{2}\)
=>Chọn C
Đúng 0
Bình luận (0)
Câu 1: \(\overrightarrow{a};\overrightarrow{b}\) cùng phương
=>\(\dfrac{2}{m}=\dfrac{-3}{1}=-3\)
=>\(m=-\dfrac{2}{3}\)
=>Chọn C
Câu 2: C
Câu 3: \(AB=\sqrt{\left(-2-1\right)^2+\left(-2-1\right)^2}=3\sqrt{2}\)
\(AC=\sqrt{\left(-7-1\right)^2+\left(-7-1\right)^2}=8\sqrt{2}\)
\(BC=\sqrt{\left(-7+2\right)^2+\left(-7+2\right)^2}=5\sqrt{2}\)
Vì AB+BC=AC
nên B nằm giữa A và C
=>Chọn B
Câu 4: A(-1;5); B(5;5); C(-1;11)
\(\overrightarrow{AB}=\left(5+1;5-5\right)\)
=>\(\overrightarrow{AB}=\left(6;0\right)\)
\(\overrightarrow{AC}=\left(-1+1;11-5\right)=\left(0;6\right)\)
=>Chọn C
Câu 5: \(\overrightarrow{AB}=\left(7-3;1+2\right)\)
=>\(\overrightarrow{AB}=\left(4;3\right)\)
\(\overrightarrow{CD}=\left(-8-0;-5-1\right)\)
=>\(\overrightarrow{CD}=\left(-8;-6\right)\)
Vì \(\dfrac{4}{-8}=\dfrac{3}{-6}\)
nên \(\overrightarrow{AB};\overrightarrow{CD}\) là hai vecto cùng phương
Vì \(\dfrac{4}{-8}=\dfrac{3}{-6}=-\dfrac{1}{2}< 0\)
nên \(\overrightarrow{AB};\overrightarrow{CD}\) là hai vecto ngược hướng
=>Chọn B
Câu 6: \(\overrightarrow{u}+\overrightarrow{v}=\left(3+1;-2+6\right)\)
=>\(\overrightarrow{u}+\overrightarrow{v}=\left(4;4\right)\)
=>\(\overrightarrow{u}+\overrightarrow{v};\overrightarrow{a}=\left(-4;4\right)\) không ngược hướng
=>A sai
\(2\overrightarrow{u}+\overrightarrow{v}=\left(2\cdot3+1;2\cdot\left(-2\right)+6\right)\)
=>\(2\overrightarrow{u}+\overrightarrow{v}=\left(7;3\right)\)
=>\(2\overrightarrow{u}+\overrightarrow{v}=\left(7;3\right);\overrightarrow{v}=\left(1;6\right)\) không cùng phương
=>Loại D
=>Chọn C
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) , điểm M thuộc cạnh BC sao cho MB=3MC. Phân tích \(\overrightarrow{AM}\) theo \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)
Ta có: MB=3MC \(\rightarrow MB=\dfrac{3}{4}BC\)
mà M nằm giữa B và C \(\rightarrow\overrightarrow{BM}=\dfrac{3}{4}\overrightarrow{BC}\)
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{3}{4}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\)
Đúng 0
Bình luận (0)
cho véc tơ a=(3;-2) vecto b= (4;1) vecto c=(0;-5)
a. Tìm u =3 vecto a -2 vecto b
b. tìm v= vecto a + 3 vecto b - 2 vec to c
c. Tìm m sao cho vecto x (m;m+1) cùng phương với vecto u
a: \(\overrightarrow{u}=3\overrightarrow{a}-2\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}x_{\overrightarrow{u}}=3\cdot3-2\cdot4=9-8=1\\y_{\overrightarrow{u}}=3\cdot\left(-2\right)-2\cdot1=-6-2=-8\end{matrix}\right.\)
Vậy: \(\overrightarrow{u}=\left(1;-8\right)\)
b: \(\overrightarrow{v}=\overrightarrow{a}+3\overrightarrow{b}-2\overrightarrow{c}\)
=>\(\left\{{}\begin{matrix}x_{\overrightarrow{v}}=3+3\cdot4-2\cdot0=3+12=14\\y_{\overrightarrow{v}}=-2+3\cdot1-2\cdot\left(-5\right)=-2+3+10=11\end{matrix}\right.\)
Vậy: \(\overrightarrow{v}=\left(14;11\right)\)
c: Để \(\overrightarrow{x};\overrightarrow{u}\) là hai vecto cùng phương thì \(\dfrac{m}{1}=\dfrac{m+1}{-8}\)
=>-8m=m+1
=>-9m=1
=>\(m=-\dfrac{1}{9}\)
Đúng 1
Bình luận (1)
Cho hình chữ nhật ABCD có AB = 3, BC = 4. Gọi M, N lần lượt là trung điểm của BC và CD. Tính:
a, độ dài của tổng ba vectơ AB, AC và AD
b, độ dài của tổng hai vectơ AM và AN
a: ABCD là hình chữ nhật
=>\(AB^2+BC^2=AC^2\)
=>\(AC=\sqrt{3^2+4^2}=5\)
ABCD là hình chữ nhật nên \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right|\)
\(=\left|\overrightarrow{AC}+\overrightarrow{AC}\right|=2\left|\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\overrightarrow{AM}+\overrightarrow{AN}\)
\(=\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{AD}+\overrightarrow{DN}\)
\(=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{DC}\)
\(=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\overrightarrow{BC}\)
\(=\dfrac{3}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{3}{2}\overrightarrow{AC}\)
=>\(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\dfrac{3}{2}\cdot AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}\)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có tâm O và E là trung điểm AD. Chứng minh rằng:
a, vectơ OA + vectơ OB + vectơ OC + vectơ OD = vectơ 0
b, vectơ EA + vectơ EB + 2 lần vectơ EC = 3 lần vectơ AB
c, vectơ AB + 2 lần vectơ EA + 4 lần vectơ ED = vectơ EC
vẽ hình giúp em với luôn ạ
a) O là tâm hbh ABCD
\(\rightarrow\) O là trung điểm AC \(\rightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\)
O là trung điểm BD \(\rightarrow\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\left(\overrightarrow{OB}+\overrightarrow{OD}\right)=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\) (đpcm)
b) Vì ABCD là hbh \(\rightarrow\overrightarrow{AB}=\overrightarrow{DC};\overrightarrow{AD}=\overrightarrow{BC}\)
Vì E là trung điểm AD \(\rightarrow\overrightarrow{EA}=\overrightarrow{DE}\)
\(2\overrightarrow{CE}=\overrightarrow{CA}+\overrightarrow{CD}\rightarrow2\overrightarrow{EC}=-\left(\overrightarrow{CA}+\overrightarrow{CD}\right)=\overrightarrow{AC}+\overrightarrow{DC}\)
Ta có: \(\overrightarrow{EA}+\overrightarrow{EB}+2\overrightarrow{EC}=\overrightarrow{DE}+\overrightarrow{EB}+\overrightarrow{AC}+\overrightarrow{DC}\)
\(=\overrightarrow{DB}+\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AB}=2\overrightarrow{AB}+\overrightarrow{DC}\)
\(=2\overrightarrow{AB}+\overrightarrow{AB}=3\overrightarrow{AB}\) (đpcm)
c) Sửa đề : CM: vectơ AB + 2 lần vectơ EA + 4 lần vectơ ED = vectơ AC
Vì E là trung điểm AD \(\rightarrow\overrightarrow{ED}=\overrightarrow{AE};\overrightarrow{AD}=2\overrightarrow{AE}\)
\(\overrightarrow{AB}+2\overrightarrow{EA}+4\overrightarrow{ED}=\overrightarrow{AB}-2\overrightarrow{AE}+4\overrightarrow{AE}=\overrightarrow{AB}+2\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
Đúng 1
Bình luận (0)