Các câu hỏi tương tự
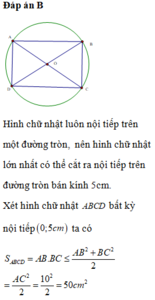
Với một miếng tôn hình tròn có bán kính bằng R9cm . Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt tạo thành hình nón bằng
Đọc tiếp
Với một miếng tôn hình tròn có bán kính bằng R=9cm . Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt tạo thành hình nón bằng
![]()
![]()
![]()
![]()
Tính diện tích lớn nhất
S
m
a
x
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R 6 cm nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp A.
S
m
a
x
...
Đọc tiếp
Tính diện tích lớn nhất S m a x của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R = 6 cm nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp

A. S m a x = 36 πcm 2
B. S m a x = 36 c m 2
C. S m a x = 96 πcm 2
D. S m a x = 18 c m 2
Cho tấm tôn hình nón có bán kính đáy là r
2
3
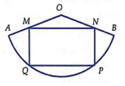
, độ dài đường sinh l 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
A
.
3
π
(...
Đọc tiếp
Cho tấm tôn hình nón có bán kính đáy là r = 2 3 , độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
A . 3 π ( 13 - 1 ) 8
B . 3 ( 13 - 1 ) 8 π
C . 5 ( 13 - 1 ) 12 π
D . π ( 13 - 1 ) 9
Cho đường tròn có bán kính bằng 4 và các nữa đường tròn có bán kính bằng 2 như hình vẽ. Khi quay hình tròn quanh cạnh AB thì các nửa đường tròn nhỏ sinh ra các khối tròn xoay có thể tích bằng bao nhiêu?
A. 71,6 π
B. 242,3 π
C. 62,5 π
Cho hình nón có đỉnh S, chiều cao h và bán kính đáy bằng R. Mặt phẳng qua S cắt hình nón tạo ra một thiết diện tam giác. Diện tích lớn nhất của thiết diện bằng:
Đọc tiếp
Cho hình nón có đỉnh S, chiều cao h và bán kính đáy bằng R. Mặt phẳng qua S cắt hình nón tạo ra một thiết diện tam giác. Diện tích lớn nhất của thiết diện bằng:
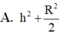
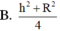
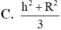
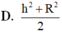
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là
a
π
R
3
b
3
(
a
,
b
∈...
Đọc tiếp
Cho hình cầu (S) tâm I bán kính R. Một mặt phẳng (P) cắt mặt cầu (S) theo đường tròn giao tuyến (L). Khối nón đỉnh I và đáy là đường tròn (L) có thể tích lớn nhất là a π R 3 b 3 ( a , b ∈ N ) . Hỏi a+ b bằng?
A. 10
B. 9
C. 11
D. 13
Cho hình hộp chữ nhật ABCD.A B C D có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 B.
8
2
C.
16
2
D.
24
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A' B' C' D' có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC' bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?
A. 8
B. 8 2
C. 16 2
D. 24 3
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu A. 4
π
(
m
2
)
B. 16
π
(
m
2
)
C. 8
π
(
m
2
)
D.
π
(
m
2...
Đọc tiếp
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu
A. 4 π ( m 2 )
B. 16 π ( m 2 )
C. 8 π ( m 2 )
D. π ( m 2 )
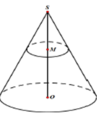
Một hình nón có chiều cao SO50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
Đọc tiếp
Một hình nón có chiều cao SO=50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM=20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
![]()
![]()
![]()
![]()