Các câu hỏi tương tự
Thả không vận tốc đầu cơ hệ như hình. Biết m1>m2, ròng rọc có dạng vành tròn khối lượng m và bỏ qua ma sát. Tính các lực căng dây
Cho hệ cơ như hình vẽ.Biết
m
1
1
k
g
;
α
30
0
,
m
2
5
k
g
,
bỏ qua ma sát giữa vật
m
2
và mặt phẳng nghiêng. Tính lực căng của sợ dây. Bỏ qua khối lượng của ròng rọc và dây nối. Coi dây không dãn trong quá trình vật chuyển động. Lấy ...
Đọc tiếp
Cho hệ cơ như hình vẽ.
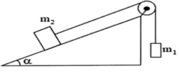
Biết m 1 = 1 k g ; α = 30 0 , m 2 = 5 k g , bỏ qua ma sát giữa vật m 2 và mặt phẳng nghiêng. Tính lực căng của sợ dây. Bỏ qua khối lượng của ròng rọc và dây nối. Coi dây không dãn trong quá trình vật chuyển động. Lấy g = 10 m / s 2
A. 12,5 N.
B. 10,5 N.
C. 7,5 N.
D. 10 N.
Cho cơ hệ như hình vẽ, vật m1, m2 nối với nhau nhờ sợi dây nhẹ, không dãn có chiều dài ℓ, ban đầu lò xo không biến dạng, đầu B của lò xo để tự do. Biết k 100 N/m, m1 400g, m2 600g, lấy g 10 π2 (m/s2). Bỏ qua mọi ma sát. Ban đầu (t 0) giữ cho m1 và m2 nằm trên mặt phẳng nằm ngang và sau đó thả cho hệ rơi tự do, khi hệ vật rơi đạt được tốc độ v0 20π (cm/s) thì giữ cố định điểm B và ngay sau đó vật m1 đi thêm được một đoạn 4cm thì sợi dây nối giữa hai vật căng. Thời điểm đầu tiên chiều dài c...
Đọc tiếp
Cho cơ hệ như hình vẽ, vật m1, m2 nối với nhau nhờ sợi dây nhẹ, không dãn có chiều dài ℓ, ban đầu lò xo không biến dạng, đầu B của lò xo để tự do. Biết k = 100 N/m, m1 = 400g, m2 = 600g, lấy g = 10 = π2 (m/s2). Bỏ qua mọi ma sát. Ban đầu (t = 0) giữ cho m1 và m2 nằm trên mặt phẳng nằm ngang và sau đó thả cho hệ rơi tự do, khi hệ vật rơi đạt được tốc độ v0 = 20π (cm/s) thì giữ cố định điểm B và ngay sau đó vật m1 đi thêm được một đoạn 4cm thì sợi dây nối giữa hai vật căng. Thời điểm đầu tiên chiều dài của lò xo cực đại là
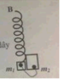
A. 0,337 s.
B. 0,314 s.
C. 0,628 s.
D. 0,323 s.
Cho cơ hệ như hình vẽ, vật m1 , m2 nối với nhau nhờ sợi dây nhẹ, không dãn có chiều dài l ban đầu lò xo không biến dạng, đầu B của lò xo đề tự do. Biết
k
100
N
/
m
,
m
1
400
g
,
m
2
600
g
lấy
g...
Đọc tiếp
Cho cơ hệ như hình vẽ, vật m1 , m2 nối với nhau nhờ sợi dây nhẹ, không dãn có chiều dài l ban đầu lò xo không biến dạng, đầu B của lò xo đề tự do. Biết k = 100 N / m , m 1 = 400 g , m 2 = 600 g lấy g = 10 = π 2 m / s 2 . Bỏ qua mọi ma sát. Ban đầu ( t = 0 ) giữ cho m 1 và m 2 nằm trên mặt phẳng nằm ngang và sau đó thả cho hệ rơi tự do, khi hệ vật rơi đạt được tốc độ v 0 = 20 π c m / s thì giữ cố định điểm B và ngay sau đó vật m 1 đi thêm được một đoạn 4cm thì sợi dây nối giữa hai vật căng. Thời điểm đầu tiên chiều dài của lò xo cực đại là
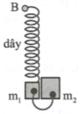
A. 0,337s
B. 0,314s
C. 0,628s
D. 0,323s
Một vật khối lượng m2=1kg được treo vào đầu một sợi dây, đầu
còn lại của sợi dây được quấn quanh một ròng rọc có dạng đĩa tròn đặc
đồng chất có thể quay quanh trục cố định đi qua tâm. Biết khối lượng
của ròng rọc là m1=2kg, bán kính R, g= 10 m/s2, bỏ qua mômen cản ở
trục quay của ròng rọc. Tính gia tốc của m2 và lực căng của dây.
Cho hệ cơ như hình vẽ bên.Biết rằng
m
1
500
g
,
m
2
1
k
g
,
hệ số lực ma sát giữa các vật với mặt sàn là
μ
1
μ
2
μ
0
,
2.
Lực kéo có độ lớn F 20N,
α
30
o...
Đọc tiếp
Cho hệ cơ như hình vẽ bên.
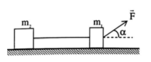
Biết rằng m 1 = 500 g , m 2 = 1 k g , hệ số lực ma sát giữa các vật với mặt sàn là μ 1 = μ 2 = μ = 0 , 2. Lực kéo có độ lớn F = 20N, α = 30 o , lấy gia tốc trọng trường g = 10 m / s 2 Tính lực căng của dây.
A. 2,44 N
B. 4,44 N.
C. 4,84 N.
D. 6,44 N.
Hai vật có khối lượng lần lượt là 2, 0 kg và 3, 0 kg được nối với nhau bằng một sợi dây rất nhẹ và vắt qua một ròng rọc có khối lượng không đáng kể. Bỏ qua mọi ma sát. Tốc độ của mỗi vật sau khi bắt đầu chuyển động được 2, 0 s gần bằng
A. 3,9 m/s. B. 11,8 m/s. C. 5,9 m/s. D. 7,8 m/s.
Một con lắc chỉ có thể dao động theo phương nằm ngang trùng với trục của lò xo, lò xo có độ cứng 100 N/m và quả cầu nhỏ dao động có khối lượng m1 100 g. Con lắc đơn gồm sợi dây dài l 25 cm và quả cầu dao động m2 giống hệt m1. Ban đầu hệ ở vị trí cân bằng phương dây treo thẳng đứng lò xo không biến dạng và hai vật m1 và m2 tiếp xúc nhau. Kéo m1 sao cho sợi dây lệch một góc nhỏ rồi buông nhẹ, biết khi qua vị trí cân bằng m1 va chạm đàn hồi xuyên tâm với m2. Bỏ qua mọi ma sát, lấy g π2 10m/s2....
Đọc tiếp
Một con lắc chỉ có thể dao động theo phương nằm ngang trùng với trục của lò xo, lò xo có độ cứng 100 N/m và quả cầu nhỏ dao động có khối lượng m1 = 100 g. Con lắc đơn gồm sợi dây dài l = 25 cm và quả cầu dao động m2 giống hệt m1. Ban đầu hệ ở vị trí cân bằng phương dây treo thẳng đứng lò xo không biến dạng và hai vật m1 và m2 tiếp xúc nhau. Kéo m1 sao cho sợi dây lệch một góc nhỏ rồi buông nhẹ, biết khi qua vị trí cân bằng m1 va chạm đàn hồi xuyên tâm với m2. Bỏ qua mọi ma sát, lấy g = π2 = 10m/s2. Chu kì dao động của cơ hệ là
A. 1,02 s
B. 0,60 s
C. 1,20 s
D. 0,81 s
Một con lắc gồm vật nặng khối lượng m treo vào đầu sợi dây dài l. Từ vị trí cân bằng kéo con lắc lệch khỏi phương thẳng đứng góc
α
0
45
°
rồi thả nhẹ. Lấy
g 10 m/s
2
.
Bỏ qua mọi ma sát. Tính gia tốc của con lắc khi lực căng dây có độ lớn bằng trọng lượng của vật. A.
10
3
m/s
2...
Đọc tiếp
Một con lắc gồm vật nặng khối lượng m treo vào đầu sợi dây dài l. Từ vị trí cân bằng kéo con lắc lệch khỏi phương thẳng đứng góc α 0 = 45 ° rồi thả nhẹ. Lấy g = 10 m/s 2 . Bỏ qua mọi ma sát. Tính gia tốc của con lắc khi lực căng dây có độ lớn bằng trọng lượng của vật.
A. 10 3 m/s 2
B. 10 6 3 m/s 2
C. 10 4 − 2 2 3 m/s 2
D. 10 5 3 m / s 2






