Chọn A.
Ta có: A(-1;2) và B(2;-1) 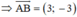
Phương trình tham số của đường thẳng đi qua A(-1;2) nhận u = (1; -1) là VTCP là: 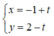
Chọn A.
Ta có: A(-1;2) và B(2;-1) 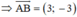
Phương trình tham số của đường thẳng đi qua A(-1;2) nhận u = (1; -1) là VTCP là: 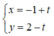
Viết phương trình đường thẳng (△):
a) đi qua M(1;2), vtcp u=(3;-4)
b) đi qua M(-2;4), vtpt n=(2;3)
c) đi qua 2 điểm A(-2;1); B(3;2)
d) đi qua M(4;-2), song song d: 3x-5y+7=0
e) đi qua N(1;-3), song song d: \(\left\{{}\begin{matrix}x-1-3t\\y=2+t\end{matrix}\right.\)
f) đi qua P(3;5), vuông góc (d): 2x-7y-1=0
g) đi qua Q(-2;0), vuông góc (d): \(\left\{{}\begin{matrix}x=2+5t\\y=1-t\end{matrix}\right.\)
h) đi qua I(1;-1) và tạo (d): x-3y+7=0 một góc α=\(\dfrac{\sqrt{2}}{10}\)
l) đi qua J(1;-1) và cách điểm K(2;3) một khoảng là \(\dfrac{19}{5}\)
cho đường thẳng △ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\)
a) viết phương trình tổng quát của đg thẳng △
b) cho đg thẳng d1: x+2y-8=0 và d2: x-2y=0. viết phương trình tổng quát của đg thẳng đi qua giao điểm của d1 với d2 và vuông góc với △
giúp mk vs ạ mk cần gấp
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
cho tam giác ABC có A(-1;2), B(-2;-1) và C(3;-2)
a) Viết phương trình tham số của đường thẳng đi qua cạnh AC
b) Viết phương trình tham số của đường trung tuyến BN
c) Viết phương trình tham số của đường cao AH
d) Viết phương trình tham số của đường trung trực đoạn AB
e) Viết phương trình tham số của đường thẳng qua A và song song BC
f) Viết phương trình tham số của đường thẳng đi qua M(3;-1) và vuông góc với OB
g) Viết phương trình tham số của đường thẳng đi qua A và song song với
(d): \(\left\{{}\begin{matrix}x=2-5t\\y=1+2t\end{matrix}\right.\)
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Cho đường thẳng d có phương trình tham số x = 2 - 3 t y = - 1 + 2 t ( t ∈ ℝ ) và điểm A(3,5 ; -2). Điểm A thuộc d ứng với giá trị nào của t ?
![]()
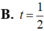
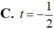
![]()
Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;1), vuông góc với đường thẳng 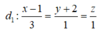 và cắt đường thẳng
d
2
: x = -1, y = t, z = 1 + t
và cắt đường thẳng
d
2
: x = -1, y = t, z = 1 + t
A. d : x - 1 = y - 1 1 = z - 1 2
B. d : x - 1 = y + 1 1 = z + 1 2
C. d : x = - t ; y = t ; z = 1 + 2 t
D. d : x 3 = y - 1 1 = z - 1 1
Phương trình tham số của đường thẳng qua M( -2; 3) và song song với đường thẳng x - 7 - 1 = y + 5 5 là:
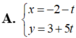
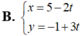
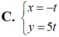
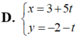
Bài 8: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:\(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\left(t\in R\right)\) và điểm A(3;1).
1) Viết phương trình đường thẳng d’ đi qua A và vuông góc với đường thẳng d.
2) Tìm tọa độ giao điểm H của đường thẳng d và d’.
3) Xác định tọa độ điểm A’ đối xứng với A qua đường thẳng d.
4) Tìm tọa độ điểm M nằm trên đường thẳng d sao cho tổng khoảng cách MA+MO là nhỏ nhất.
5) Viết phương trình đường tròn (C) có tâm I nằm trên đường thẳng d và đi qua hai điểm A, O.