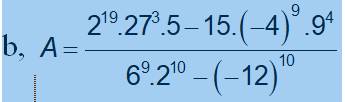\(a.2^{x+2}-2^x=96\\ 2^x\cdot4-2^x=96\\ 2^x\cdot\left(4-1\right)=96\\ 2^x\cdot3=96\\ 2^x=96:3\\ 2^x=32\\ 2^x=2^5\\ =>x=5\)
\(2^{x+1}\cdot3^y=12^x\\ 2^{x+1}\cdot3^y=3^x\cdot2^{2x}\\ \left\{{}\begin{matrix}2^{x+1}=2^{2x}\\3^y=3^x\end{matrix}\right.\\ \left\{{}\begin{matrix}x+1=2x\\y=x\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=x=1\end{matrix}\right.\\ \left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(c.10^x:5^y=20^y\\ 10^x:5^y=5^y\cdot4^y\\ 10^x=10^{2y}\\ =>x=2y\)

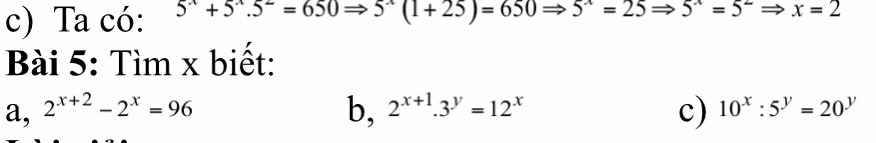







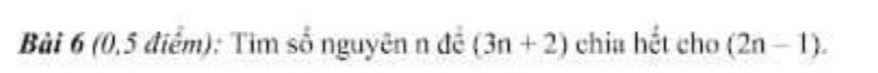 mn giúp em với ạ, em đang cần gấp lắm ạ
mn giúp em với ạ, em đang cần gấp lắm ạ