Các câu hỏi tương tự
Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152
m
2
và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường). A. 16m x 24m B. 8m x 48m C. 12m x 32m D. 24m x 32m
Đọc tiếp
Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152 m 2 và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường).
A. 16m x 24m
B. 8m x 48m
C. 12m x 32m
D. 24m x 32m
Mọt cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Các kích thước được ghi cùng đơn vị. Hãy tính thể tích của bồn chứa A.
π
4
2
.
3
5
B.
π
4
5
.
3
2
C.
π
4
2...
Đọc tiếp
Mọt cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Các kích thước được ghi cùng đơn vị. Hãy tính thể tích của bồn chứa
A. π 4 2 . 3 5
B. π 4 5 . 3 2
C. π 4 2 3 5
D. π 4 5 3 2
Một chiếc hộp hình chữ nhật có kích thước
6
c
m
×
6
c
m
×
10
c
m
Người ta xếp những cây bút chì chưa vuốt có hình lăng trụ lục giác đều (đang để lộn xộn như trong ảnh dưới đây) với chiều dài 10 cm và thể tích
1875
3
2
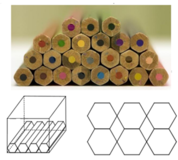
vào trong hộp sao cho chúng được xếp sát nhau (như hình vẽ mô phỏng phía dưới) . Hỏi có thể chứa được tối đa b...
Đọc tiếp
Một chiếc hộp hình chữ nhật có kích thước 6 c m × 6 c m × 10 c m Người ta xếp những cây bút chì chưa vuốt có hình lăng trụ lục giác đều (đang để lộn xộn như trong ảnh dưới đây) với chiều dài 10 cm và thể tích 1875 3 2 vào trong hộp sao cho chúng được xếp sát nhau (như hình vẽ mô phỏng phía dưới) . Hỏi có thể chứa được tối đa bao nhiêu cây bút chì ?
A. 144
B. 156
C. 221
D. 576
Có nhiều tờ giấy chồng nhau, mỗi tờ có bề dày là 0,1 mm. Ta xếp chồng liên tiếp tờ này lên tờ khác (h.48). Giả sử có thể thực hiện việc xếp giấy như vậy một cách vô hạn.Gọi u1 là bề dày của một tờ giấy,
u
2
là bề dày của một xếp giấy gồm hai tờ,
u
3
là bề dày của một xếp giấy gồm ba tờ, …,
u
n
là bề dày của một xếp giấy gồm n tờ. Tiếp tục như vậy t được dãy số vô...
Đọc tiếp
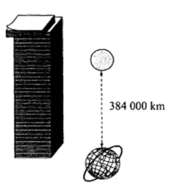
Có nhiều tờ giấy chồng nhau, mỗi tờ có bề dày là 0,1 mm. Ta xếp chồng liên tiếp tờ này lên tờ khác (h.48). Giả sử có thể thực hiện việc xếp giấy như vậy một cách vô hạn.
Gọi u1 là bề dày của một tờ giấy, u 2 là bề dày của một xếp giấy gồm hai tờ, u 3 là bề dày của một xếp giấy gồm ba tờ, …, u n là bề dày của một xếp giấy gồm n tờ. Tiếp tục như vậy t được dãy số vô hạn ( u n ).
Bảng sau đây cho biết bề dày (tính theo mm) của một số chồng giấy.

a) Quan sát bảng trên và nhận xét về giá trị của u n khi n tăng lên vô hạn.
b) Với n như thế nào thì ta đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng? (Cho biết khoảng cách này ở một thời điểm xác định là 384000 km hay 384 . 10 9 m m
Một hình trụ có tâm các đáy là A,B. Biết rằng mặt cầu đường kính AB tiếp xúc với các mặt, đáy của hình trụ tại A,B và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là
16
π
. Tính diện tích xung quanh của mặt trụ đã cho.
A
.
16
π
3
B
.
16
π
C
.
8...
Đọc tiếp
Một hình trụ có tâm các đáy là A,B. Biết rằng mặt cầu đường kính AB tiếp xúc với các mặt, đáy của hình trụ tại A,B và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 16 π . Tính diện tích xung quanh của mặt trụ đã cho.
A . 16 π 3
B . 16 π
C . 8 π
D . 8 π 3
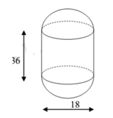
Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao 36dm (như hình vẽ). Tính thể tích V của cái bồn đó A. V 9216
π
dm
3
B. V
1024
π
9
d
m
3
C. V
16
π
243
...
Đọc tiếp
Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao 36dm (như hình vẽ). Tính thể tích V của cái bồn đó
A. V = 9216 π dm 3
B. V = 1024 π 9 d m 3
C. V = 16 π 243 d m 3
D. V = 3888 d m 3
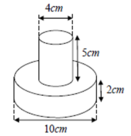
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OA OB. Khi đó tỉ số thể tích của hai hình nón
V
n
và thể tích hình trụ
V
t
bằng:
A
.
1
2
B
.
1
4
C
.
2
5
D...
Đọc tiếp
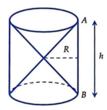
Hình bên cho ta ảnh của một đồng hồ cát với kích thước kèm theo OA = OB. Khi đó tỉ số thể tích của hai hình nón V n và thể tích hình trụ V t bằng:
A . 1 2
B . 1 4
C . 2 5
D . 1 3
Cho hình lập phương có cạnh bằng 40 cm và một hình trụ có hai đáy là hai hai hình tròn nội tiếp hai mặt đối điện của hình lập phương (tham khảo hình vẽ bên). Gọi
S
1
,
S
2
lần lượt là diện tích toán phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S
S
1
+...
Đọc tiếp
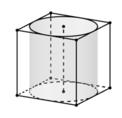
Cho hình lập phương có cạnh bằng 40 cm và một hình trụ có hai đáy là hai hai hình tròn nội tiếp hai mặt đối điện của hình lập phương (tham khảo hình vẽ bên). Gọi S 1 , S 2 lần lượt là diện tích toán phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S= S 1 + S 2 ( c m 2 )
A. S=4(2400 + π )
B. S=4(2400 + 3 π )
C. S=2400(4 + π ).
D. S=2400(4 + 3 π )
Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a
3
là được thiết diện là hình vuông có diện tích bằng
4
a
2
Tính thể tích V của khối trụ (T)?.
Đọc tiếp
Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a 3 là được thiết diện là hình vuông có diện tích bằng 4 a 2 Tính thể tích V của khối trụ (T)?.
![]()

![]()