Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)
Câu 8:
c.
$xy-3x+y=15$
$\Rightarrow x(y-3)+(y-3)=12$
$\Rightarrow (x+1)(y-3)=12$
Do $x,y$ nguyên nên $x+1, y-3$ nguyên. Mà $(x+1)(y-3)=12$ nên ta xét các TH sau:
TH1: $x+1=1, y-3=12\Rightarrow x=0; y=15$ (tm)
TH2: $x+1=-1; y-3=-12\Rightarrow x=-2; y=-9$ (tm)
TH3: $x+1=12; y-3=1\Rightarrow x=11; y=4$ (tm)
TH4: $x+1=-12; y-3=-1\Rightarrow x=-13; y=2$ (tm)
TH5: $x+1=2; y-3=6\Rightarrow x=1; y=9$ (tm)
TH6: $x+1=-2; y-3=-6\Rightarrow x=-3; y=-3$ (tm)
TH7: $x+1=6; y-3=2\Rightarrow x=5; y=5$ (tm)
TH8: $x+1=-6; y-3=-2\Rightarrow x=-7; y=1$ (tm)
TH9: $x+1=3; y-3=4\Rightarrow x=2; y=7$ (tm)
TH10: $x+1=-3; y-3=-4\Rightarrow x=-4; y=-1$ (tm)
TH11: $x+1=4, y-3=3\Rightarrow x=3; y=6$ (tm)
TH12: $x+1=-4; y-3=-3\Rightarrow x=-5; y=0$ (tm)

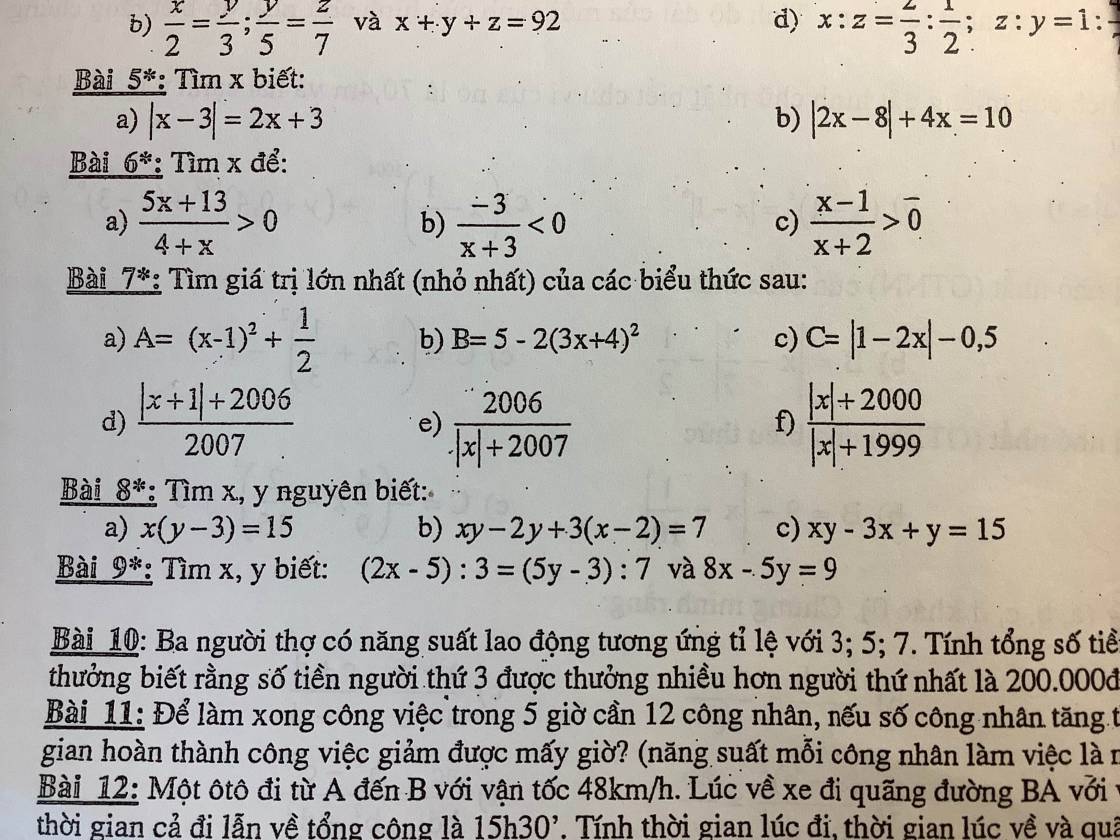




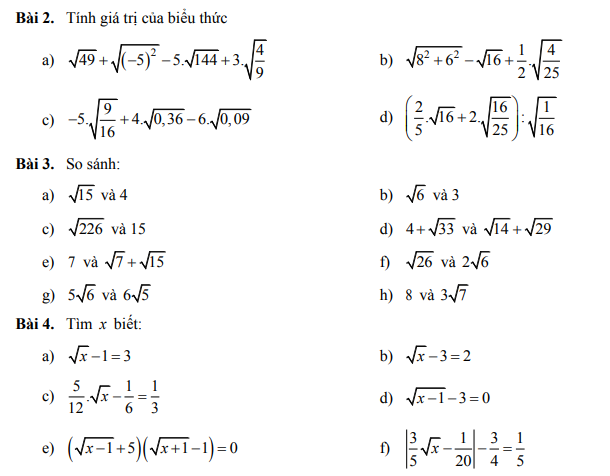 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy

 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
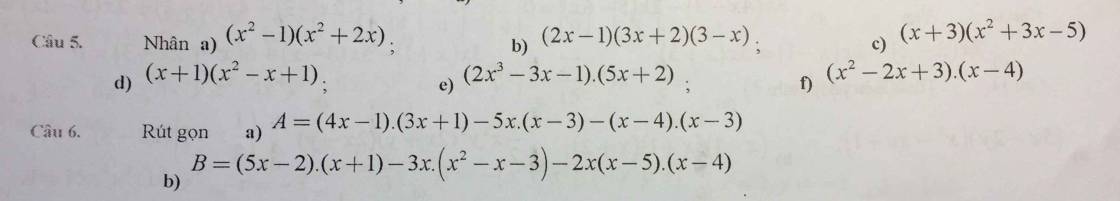

 lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!!
lm giúp mk bài 3 với bài 4 với ạ, mk đng cần gấp, cảm ơn mn rất rất nhiều ạ !!!! giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !