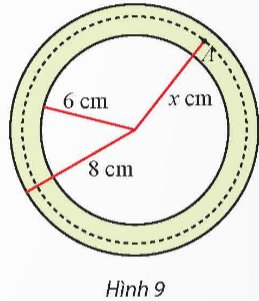
Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9. Khí bên trong ống được duy trì ở 150°C. Biết rằng nhiệt độ T(°C) tại điểm A trên thành ống là hàm số của khoảng cách x (cm) từ A đến tâm của mặt cắt và T′(x) = \(-\dfrac{30}{x}\) (6 ≤ x ≤ 8).
(Nguồn: Y.A.Cengel, A.I.Gahjar, Heat and Mass Transfer, McGraw Hill, 2015)
Tìm nhiệt độ mặt ngoài của ống.
Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\).
Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\).
Ta có \(\int\limits_6^8 {T'\left( x \right)dx} = \int\limits_6^8 { - \frac{{30}}{x}dx} = - 30\int\limits_6^8 {\frac{1}{x}dx = - 30.\left. {\left( {\ln \left| x \right|} \right)} \right|_6^8 = - 30\ln 8 + 30\ln 6} \).
Vậy nhiệt độ bên ngoài mặt ống là \(T\left( 8 \right) = - 30\ln 8 + 30\ln 6 + 150 \approx 141,{37^o}C\)


