a, Theo tính chất tiếp tuyến cắt nhau => AB = AC => A thuộc trung trực của BC.
OB = OC => O thuộc trung trực của BC
b, Sử dụng a) và chú ý CD là đường kính (O) nên C B D ^ = 90 0
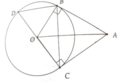
Từ điểm A ở ngoài đường tròn (O,R) vẽ hai tiếp tuyến AB và AC đến (O,R), với B và C là các tiếp điểm. Tia AO cắt dây BC tại H.
a) Chứng minh OA là trung trực của đoạn thẳng BC và AB2 = AH . AO
b) Vẽ đường kính BD của (O,R). Gọi M là trung điểm CD. Tiếp tuyến tại D của (O) cắt BC tại E. Chứng minh ∆DME ~ ∆BOE.
c) Tia EM cắt BD tại K, tia EO cắt CD tại I. Chứng minh IK ⊥ OD.
Từ điểm A nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB và AC với đường tròn (O;R) . Gọi H là giao điểm của AO và BC.
a) Chứng minh AO là đường trung trực BC
b) Vẽ đường kính CD của đường tròn (O) , AD cắt đường tròn (O) tại E. Chứng minh \(AB^2=AE.AD\)
c) Tiếp tuyến E của đường tròn (O) cắt AB , AC lần lượt tại M và N . Chứng minh chu vi \(\Delta ANM=AB+AC\)
d) MN cắt AO tại I , EO cắt BC tại P . Chứng minh \(AE//IP\)
Bài 1. Từ điểm
A
ở ngoài đường tròn
(O R; )
, vẽ hai tiếp tuyến
AB AC ,
đến
(O R; )
với
BC,
là các tiếp
điểm. Tia
AO
cắt dây
BC
tại
H .
a)Chứng minh:
OA
là đường trung trực của đoạn thẳng BC và
2 AB AH AO =
.
b)Vẽ đường kính
BD
của
(O R; )
. Gọi
M
là trung điểm của
CD
. Chứng minh
OMCH
là hình
chữ nhật.
Cho đường tròn (O,R) và điểm A ở ngoài đường tròn với OA>2R. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B,C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC;AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.
a) Chứng minh: A,B,C,O,M cùng thuộc một đường tròn và SC^2=SB.SD
b) Tia BM cắt (O) tại K khác B. Chứng minh: CK song song với DE.
c) Chứng minh tứ giác MKCD là một hình bình hành.
d) Hai đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H.
Chứng minh: Ba điểm H, O, C thẳng hàng.
Cho (O;R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A và B vẽ 2 tiếp tuyến AB, AC của đường tròn O (B,C là các tiếp điểm). VẼ dây BE của đường tròn O song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của DE. Hai đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H. Chứng minh 3 điểm H,O,C thẳng hàng.
Cho đường tròn (O) và 1 điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B, C là các tiếp điểm). AO cắt BC tại D
a/ Chứng minh tam giác ABC cân tại A và AO là đường trung trực của BC
b/ Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh tam giác AGO đồng dạng tam giác HDO
c/ Chứng minh EH là tiếp tuyến của đường tròn (O)
1. Cho các đường tròn (O;R) và (O';R') tiếp xúc trong với nhau tại A(R>R'). Vẽ đường kính AB của (O) , AB cắt (O') tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O'), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a) AP là phân giác của góc BAQ
b) CP và BR song song với nhau
2. Cho đường tròn (O;R) vơi SA là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). gọi I là trung điểm MA, K là giao điểm của BI với (O)
a) Chứng minh các tam giác IKA và IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB
b) Giả sử MK cắt (O) tại C. Chứng minh BC song song MA
3. Cho tam giác ABC nội tiếp đường tròn (O) và AB<AC. Đường tròn (I) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh OA và BD vuông góc với nhau.
4.Cho hai đường tròn (O) và (I) cắt nhau tại C và D, trong đó tiếp tuyến chung MN song song với cát tuyến EDF, M và E thuộc (O), N và F thuộc (I), D nằm giữa E và F. Gọi K ,H theo thứ tự là giao điểm của NC,MC và EF. Gọi G là giao điểm của EM ,FN. Chứng minh:
a) Các tam giác GMN và DMN bằng nhau
b) GD là đường trung trực của KH
Làm ơn giúp mình với !!! Chút nữa là mình đi học rồi !!!! Cảm ơn trước !!!
Cho (O; 3) đường kính BD, A nằm ngoài đường tròn. Kẻ tiếp tuyến AB,AC với đường tròn( B,C là các tiếp điểm)
a) Chứng minh AO vuông góc với BC và AO//CD
b) Tính chu vi và diện tích tam giác ABC
c) Qua O, kẻ đường thẳng vuông góc với BD cắt tia CD tại E, đường thẳng AE và OC cắt nhau tại I, đường thẳng OE và AC cắt nhau tại G. Chứng minh IG là trung trực của OA
Giải dùm mk nha, mk cần gấp
Cho đường tròn (o). Từ điểm A ở ngoài đường tròn vẽ hai tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm). Gọi H là giao điểm của AO và BC
A) Chứng minh H là trung điểm của BC
B) kẻ đường kính BD của đường tròn (o). Chứng minh DC// AO
