a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH=\dfrac{6^2}{10}=3,6\left(cm\right)\)
b: Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>EF=AH
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot CH=AH^2\)
mà AH=EF
nên \(HB\cdot HC=EF^2\)
c: Xét ΔBEH vuông tại E có \(cosB=\dfrac{BE}{BH}\)
Xét ΔBHA vuông tại H có \(cosB=\dfrac{BH}{BA}\)
Xét ΔBAC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
\(cosB\cdot cosB\cdot cosB=\dfrac{BE}{BH}\cdot\dfrac{BH}{BA}\cdot\dfrac{BA}{BC}\)
=>\(cos^3B=\dfrac{BE}{BC}\)
=>\(BE=BC\cdot cos^3B\)









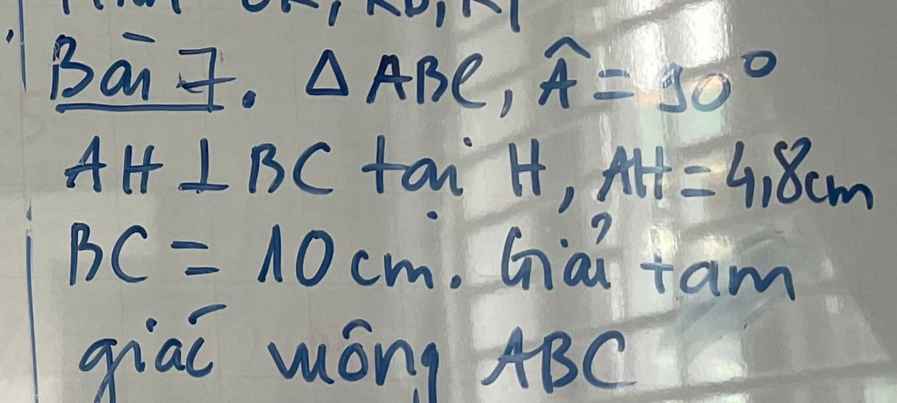

 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp








