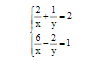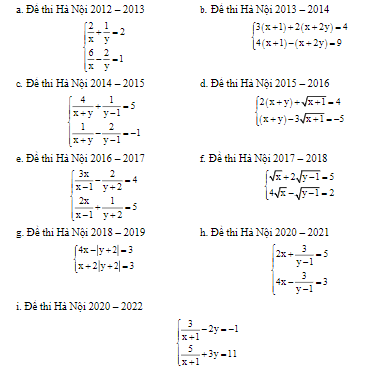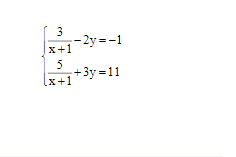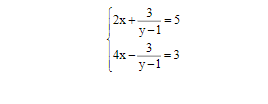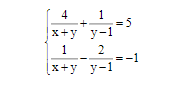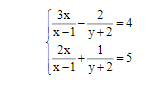\(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{1}{y}=2.\\\dfrac{6}{x}-\dfrac{2}{y}=1.\end{matrix}\right.\left(ĐK:x\ne0;y\ne0\right).\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\left(a\ne0;b\ne0\right).\)
\(\Rightarrow\left\{{}\begin{matrix}2a+b=2.\\6a-2b=1.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+2b=4.\\6a-2b=1.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=2.\\10a=5.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1.\\a=\dfrac{1}{2}.\end{matrix}\right.\left(TM\right).\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=1.\\\dfrac{1}{x}=\dfrac{1}{2}.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=1.\\x=2.\end{matrix}\right.\) \(\left(TM\right).\)
Vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(2;1\right).\)