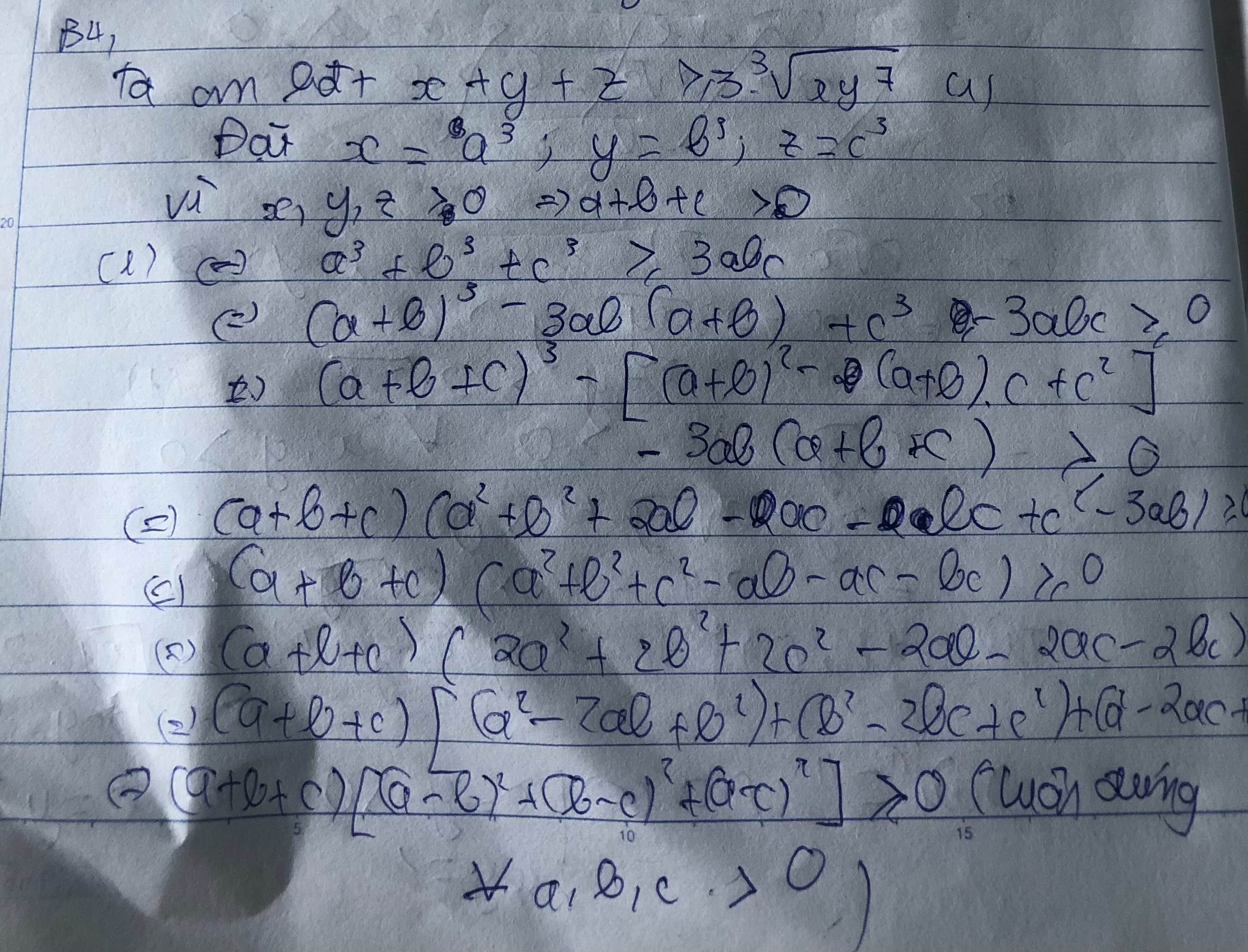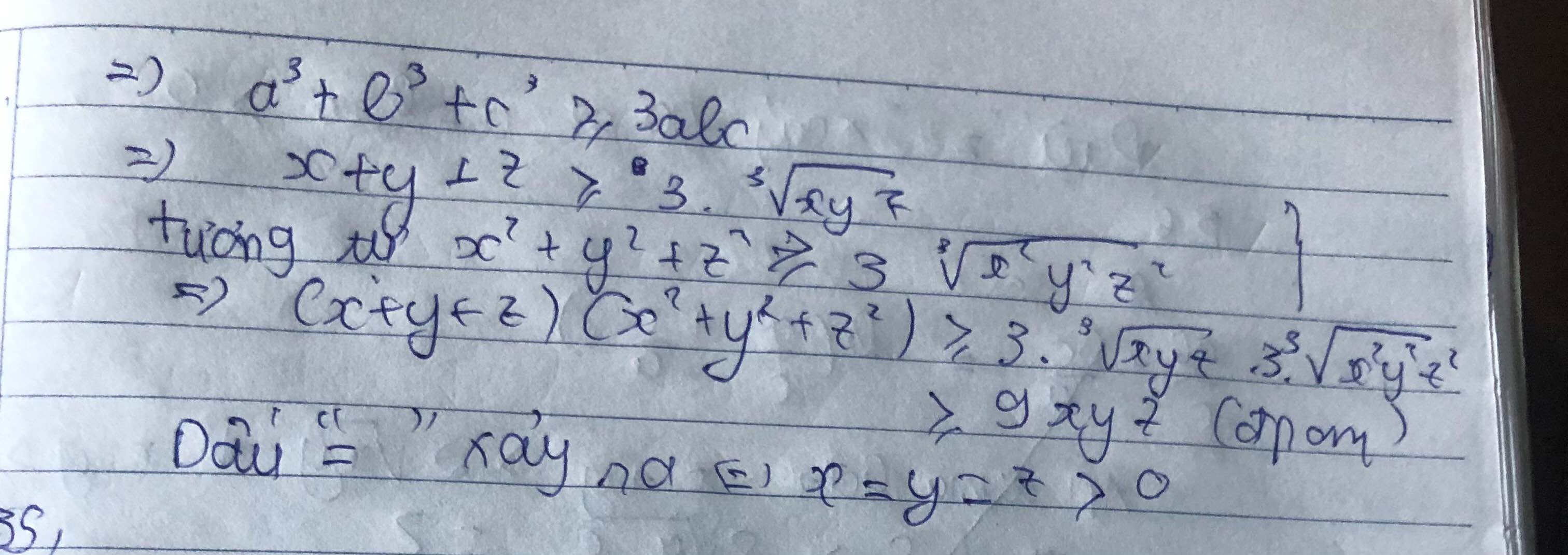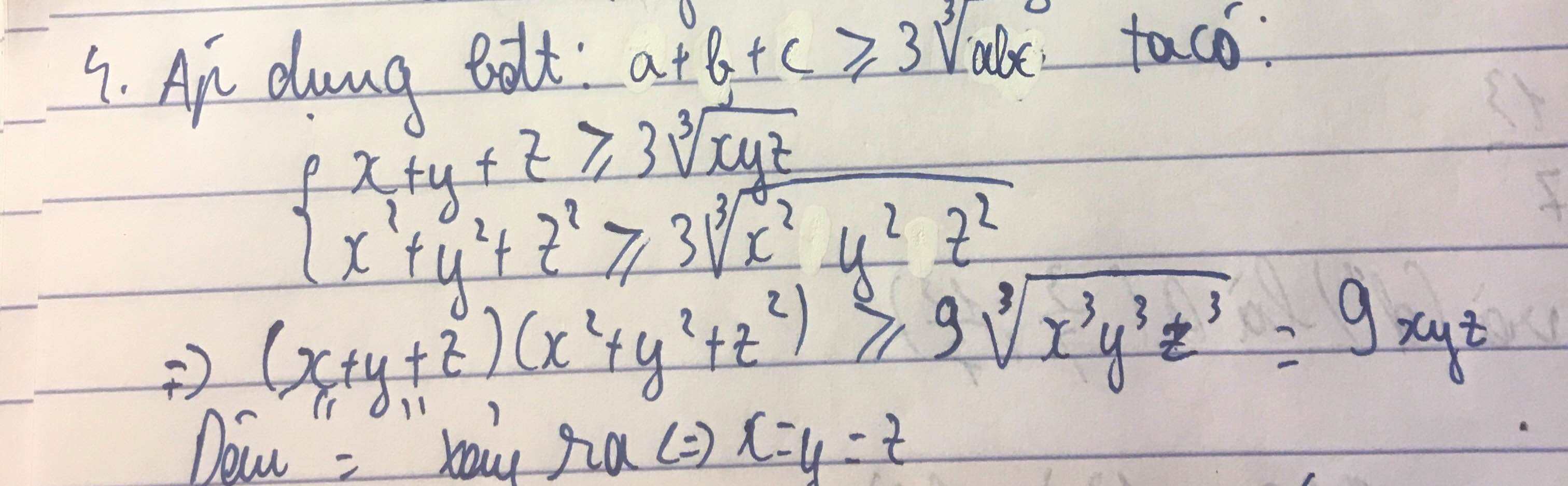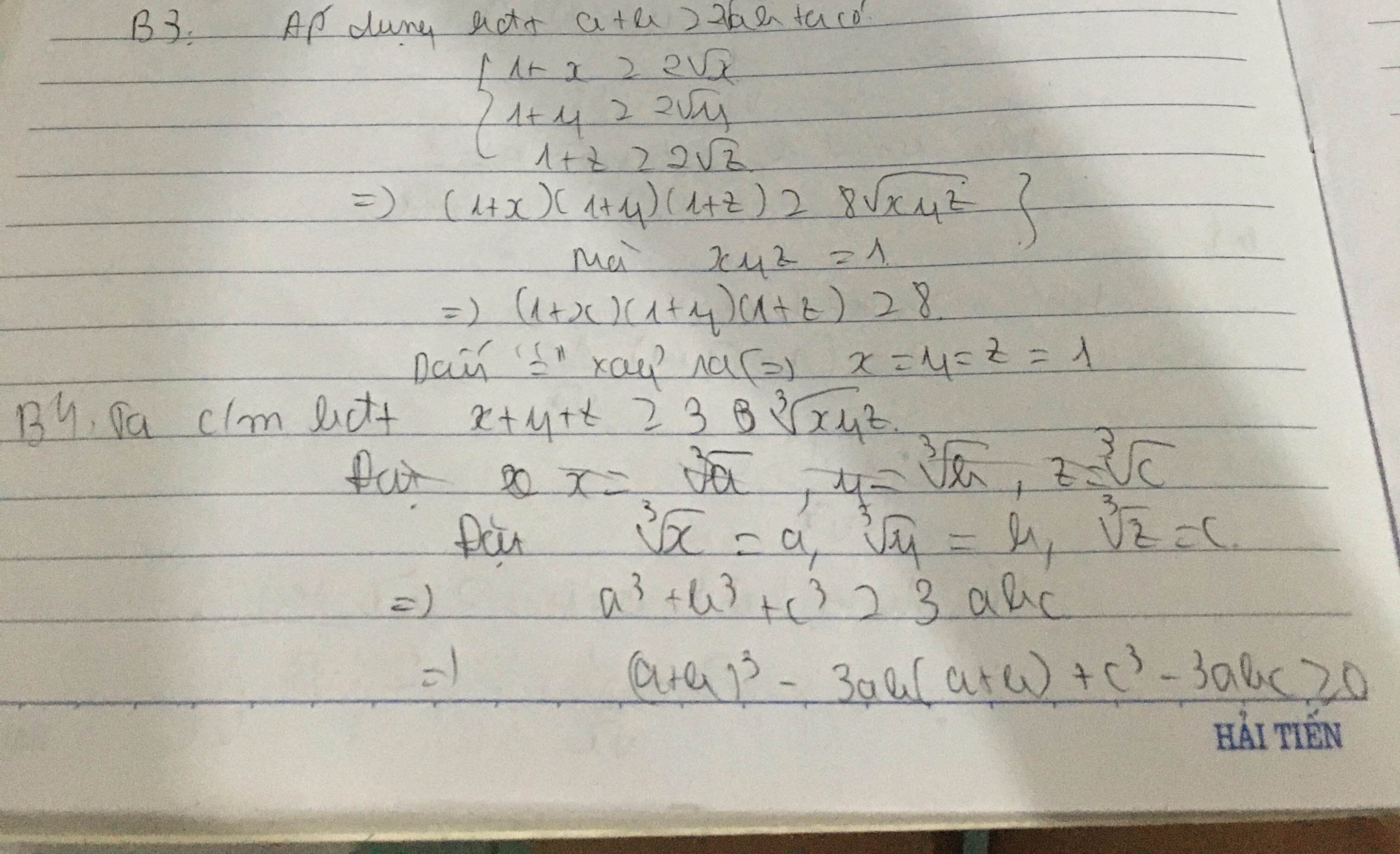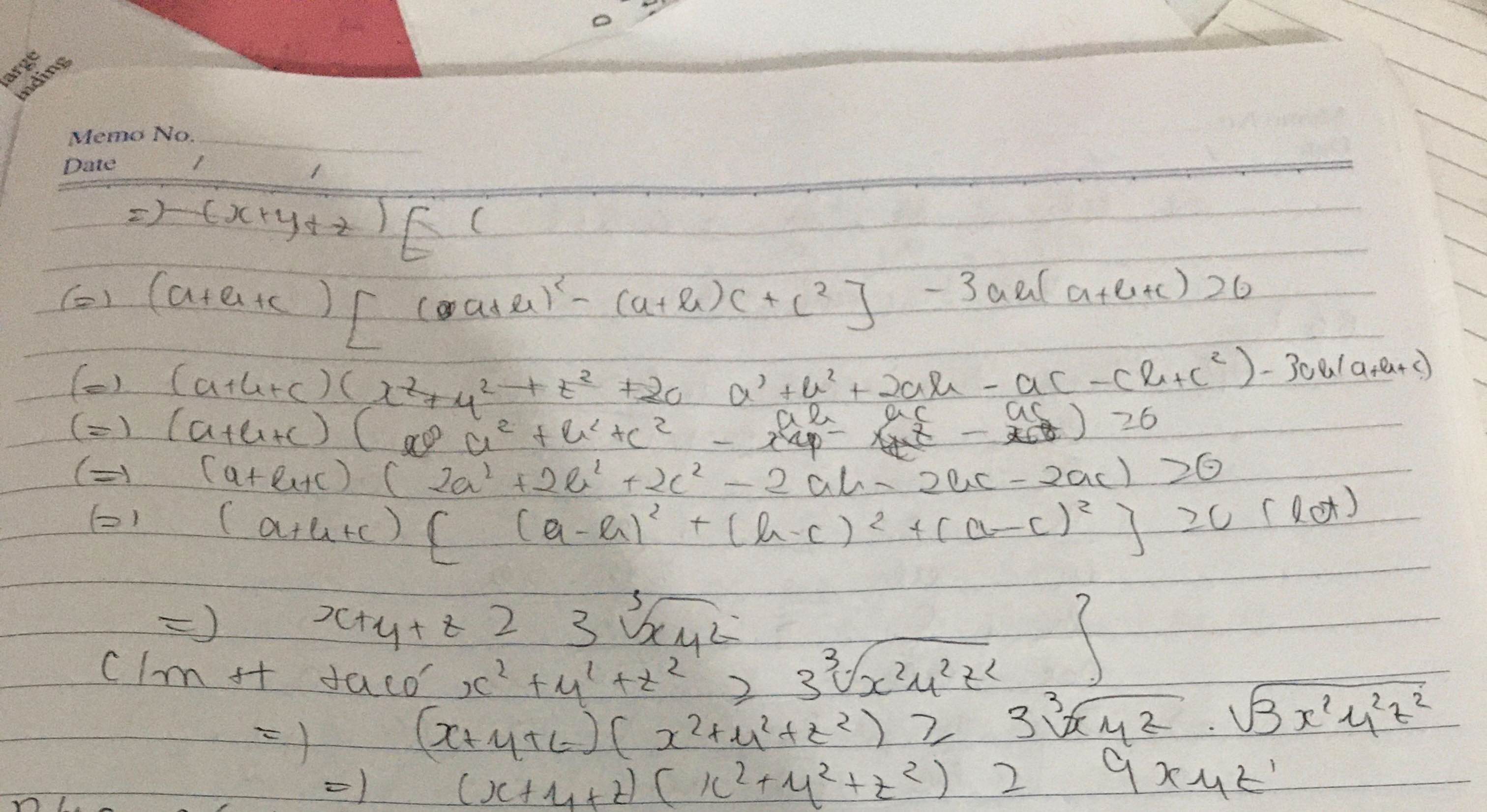Question

Cho \(x,y,z\)  là ba số dương. Chứng minh rằng

     \(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge9xyz\).

Answer 1

Sử dụng bất đẳng thức Cô si cho ba số dương ta có

                    x+y+z\ge3\sqrt[3]{xyz}x+y+z≥33xyz​  và    x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}x2+y2+z2≥33x2y2z2​

Nhân theo vế hai bất đẳng thức này ta suy ra được đpcm.

Đẳng thức xảy ra khi và chỉ khi  x=y=zx=y=z.

Answer 2

Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)\left[\frac{\left(x+y+z\right)^2}{3}\right]=\frac{\left(x+y+z\right)^3}{3}\)(1)

Áp dụng bất đẳng thức AM-GM ta có : 

\(x+y+z\ge3\sqrt[3]{xyz}\)=> \(\left(x+y+z\right)^3\ge27xyz\)=> \(\frac{\left(x+y+z\right)^3}{3}\ge9xyz\)(2)

Từ (1) và (2) => \(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge\frac{\left(x+y+z\right)^3}{3}\ge9xyz\)

=> \(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge9xyz\left(đpcm\right)\)

Đẳng thức xảy ra <=> x=y=z

Answer 3

Áp dụng bất đẳng thức Cô si ta được 

x+y+z ≥ \(3\sqrt[3]{xyz}\)

\((x)^{2}+(y)^{2}+(z)^{2}\) ≥ \(3\sqrt[2]{x^2y^2z^2}\)

Nhân theo vế hai bất đẳng thức này ta suy ra được đpcm 

Đẳng thức này xảy ra <=> x=y=z

 

Answer 4

Sử dungk bất đẳng thức Cô si cho ba số dương ta có :

x+y+z>= 3\(\sqrt[3]{xyz}\)$v$à \(x^2\)+\(y^2\)+\(z^2\)>=3\(\sqrt[3]{x^2y^2z^2}\)

Nhân theo vế hai bất đẳng thức này ta suy ra được đpcm.

Đẳng thức xảy ra khi và chỉ khi  $x=y=z$.

                  

Answer 5

Answer 6

 

Sử dụng bất đẳng thức Cô si cho ba số dương ta có

                    x+y+z\ge3\sqrt[3]{xyz}x+y+z≥33xyz​  và    x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}x2+y2+z2≥33x2y2z2​

Nhân theo vế hai bất đẳng thức này ta suy ra được đpcm.

Đẳng thức xảy ra khi và chỉ khi  $x=y=z$.

Answer 7

x=y=z

Answer 8

Bất đẳng thức Cô si ta cho 3 số dương ta có x + y + z≥ 3\(\sqrt[3]{xyz}\)

x² + y² + z² ≥ 3\(\sqrt[3]{x^{ }2y^{ }2z^{ }2}\)

( x + y + z)(x² + y² + z² )≥9xyz (đpcm)

Đẳng thức chỉ xảy ra khi và chỉ khi x=y=z

Answer 9

Answer 10

Áp dụng BĐT Cô-si cho ba số dương x, y, z, ta được \(x+y+z\ge3\sqrt[3]{xyz}\)

Tương tự, ta có: \(x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}\)

Nhân vế theo vế của các BĐT trên, ta được:

\(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge3\sqrt[3]{xyz}.3\sqrt[3]{x^2y^2z^2}=9\sqrt[3]{xyzx^2y^2z^2}=9\sqrt[3]{x^3y^3z^3}=9xyz\)

Vậy với x, y, z > 0 thì \(\left(x+y+z\right)\left(x^2+y^2+z^2\right)\ge9xyz\)

Answer 11

    

Answer 12

  

Answer 13

    

Answer 14

Áp dụng bất đẳng thức Cô-si cho ba số a, b, c (a, b, c > 0), ta có:

x + y + z ≥ 3\(\sqrt[3]{xyz}\)

Tương tự: \(x^2+y^2+z^2\ge3\sqrt[3]{x^2y^2z^2}\)

⇒(x + y + z )(\(x^2+y^2+z^2\)) ≥ 3\(\sqrt[3]{xyz}\) . 3\(\sqrt[3]{x^2y^2z^2}\)

⇒(x + y + z )(\(x^2+y^2+z^2\)) ≥ 9\(\sqrt[3]{x^3y^3z^3}\)

⇒(x + y + z )(\(x^2+y^2+z^2\)) ≥ 9xyz