Cho tam giác ABC vuông tại A lấy điểm M là trung điểm của AC Trên tia đối của tia MB lấy điểm D sao cho MD = MB.
a) chứng minh rằng tam giác ABC bằng tam giác CDM
. b) so sánh độ dài BC và BA Từ đó so sánh độ dài BC và CD.
c) Trên tia đối của tia CA lấy điểm E sao cho CE = CA. Gọi I là trung điểm của De. Chứng minh rằng ba điểm B,C,I thẳng hàng.
Theo dõi Báo cáo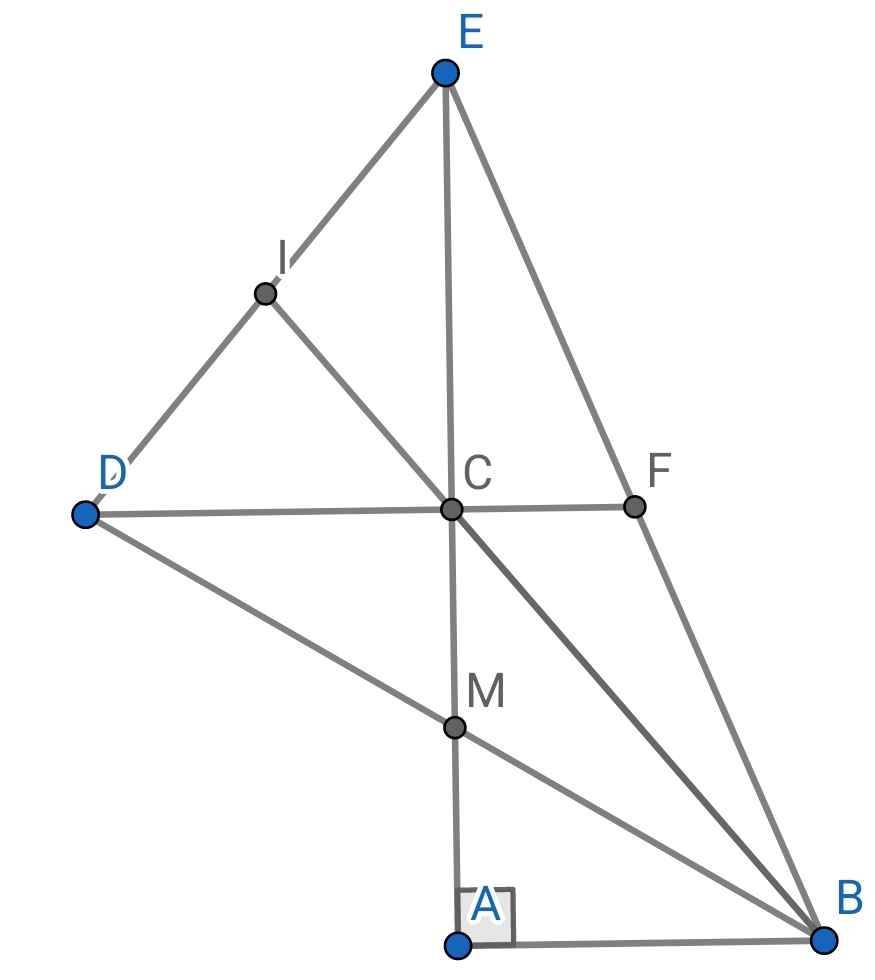
a) Sửa đề: Chứng minh ∆ABM = ∆CDM
Do M là trung điểm của AC (gt)
⇒ MA = MC
Xét ∆ABM và ∆CDM có:
BM = DM (gt)
∠AMB = ∠CMD (đối đỉnh)
MA = MC (cmt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) ∆ABC vuông tại A (gt)
⇒ BC là cạnh huyền nên là cạnh lớn nhất
⇒ BC > BA
Do ∆ABM = ∆CDM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà BC > BA (cmt)
⇒ BC > CD
c) Do ∆ABM = ∆CDM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ CD ⊥ AE
Gọi F là giao điểm của CD và BE
⇒ CF ⊥ AE
Xét hai tam giác vuông: ∆FCA và ∆FCE có:
CA = CE (gt)
CF là cạnh chung
⇒ ∆FCA = ∆FCE (hai cạnh góc vuông)
⇒ ∠CFA = ∠CFE (hai góc tương ứng)
⇒ FC là tia phân giác của ∠AFE
∆FAE có:
FC là đường cao (do FC ⊥ AE)
FC là đường phân giác (cmt)
⇒ ∆FAE cân tại F
⇒ FA = FE
Do AB // CD (cmt)
⇒ AB // CF
⇒ ∠FAB = ∠CFA (so le trong)
∠FBA = ∠CFE (đồng vị)
Mà ∠CFA = ∠CFE (cmt)
⇒ ∠FAB = ∠FBA
⇒ ∆FAB cân tại F
⇒ FA = FB
Mà FA = FE (cmt)
⇒ FB = FE
⇒ F là trung điểm của BE
Do MB = MD (gt)
⇒ M là trung điểm của BD
∆BDE có:
DF là đường trung tuyến của ∆BDE (do F là trung điểm của BE)
EM là đường trung tuyến của ∆BDE (do M là trung điểm của BD)
Mà DF và EM cắt nhau tại C
⇒ BC là đường trung tuyến thứ ba của ∆BDE
Lại có:
I là trung điểm của DE (gt)
⇒ B, C, I thẳng hàng (tính chất ba đường trung tuyến của tam giác)