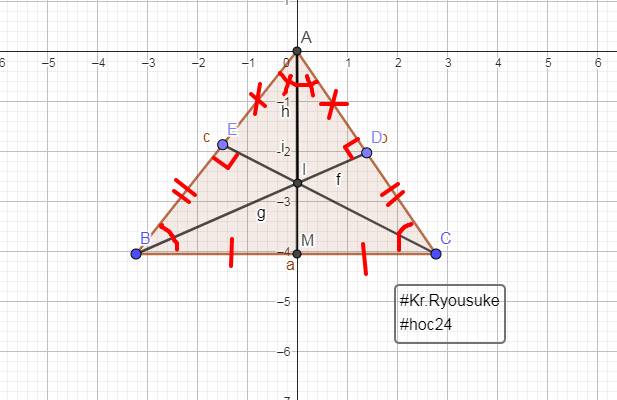
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
=>BE=DC
=>AE=AD
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
=>ΔAEI=ΔADI
=>góc EAI=góc DAI
=>AI là phân giác của góc BAC
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
=>A,I,M thẳng hàng
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `2\Delta` vuông và `BEC` và `CDB`:
`\text {BC chung}`
$\widehat {B} = \widehat {C}$
`=> \Delta BEC = \Delta CDB (ch-gn)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AE + BE}\\\text{AC = AD + CD}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CD}\end{matrix}\right.\)
`-> \text {AE = AD}`
Xét `2\Delta` vuông `AEI` và ` ADI`:
`\text {AE = AD}`
`\text {AI chung}`
`=> \Delta AEI = \Delta ADI (ch-cgv)`
`->` $\widehat {EAI} = \widehat {DAI} (\text {2 góc tương ứng})$
`-> \text {AI là tia phân giác của}` $\widehat {EAD}$
Mà \(\text{E}\in\text{AB, D}\in\text{AC}\)
`-> \text {AI là tia phân giác của}` $\widehat {BAC}$ `(1)`
`c,`
Vì M là trung điểm của AC
`-> \text {AM là đường trung tuyến của} \Delta ABC` `(2)`
Từ `(1)` và `(2)`
`-> \text {Ba điểm A, I, M thẳng hàng.}`