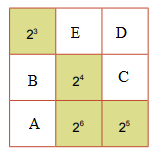
Ta đặt các ô chưa biết như sau:
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là: