Chọn A.
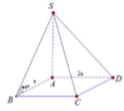
Ta có: ![]()
![]() Do tam giác SAB vuông cân tại A nên SA = AB = a.
Do tam giác SAB vuông cân tại A nên SA = AB = a.
Vậy ![]()
Chọn A.

Ta có: ![]()
![]() Do tam giác SAB vuông cân tại A nên SA = AB = a.
Do tam giác SAB vuông cân tại A nên SA = AB = a.
Vậy ![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
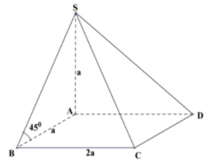
A. 6 a 3 18
B. 2 2 a 3 3
C. a 3 3
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; AD=2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
A. 30 0
B. 60 0
C. 45 0
D. 75 0
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh AB=a, AD=a 3 . Cạnh bên SA=a 2 và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SAC)
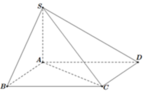
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy AB=a, AD=a 2 , SA=a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 300
B. 450
C. 600
D. 750
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, cạnh bên SA vuông góc với mặt đáy, SA = a. Gọi H là hình chiếu của a trên SB, tính thể tích khối chóp H.ABCD theo a và côsin của góc giữa 2 mặt phẳng (SBC) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB=2a, AD=a 3 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy là 30 ° . Diện tích mặt cầu ngoại tiếp hình chóp là:
![]()
![]()
![]()
![]()
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và cạnh bên SB tạo với đáy một góc 45°. Thể tích khối chóp S.ABCD bằng:
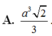
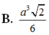
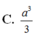
![]()
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.