a: XétΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
c: AE=EH
EH<EC
=>AE<EC
cho tam giác ABC vuông tại A có AB=AC gọi K là trung điểm của cạnh BC
a,Chứng minh Tam giác AKB=Tam giác AKC và AK vuông góc BC
b,Từ C kẻ đường vuông góc với BC cắt AB tại E.Chứng minh AK//CE và CE=CB
c, So sánh AK và CE
câu1
\(\dfrac{a}{2}\)= \(\dfrac{b}{7}\)=\(\dfrac{c}{3}\)và 2a +b-c =54
câu2
cho ΔABC vuông tại A .Vẽ tia phân giác BD của Abc (D ϵ AC) . KẺ DE vuông góc với BC tại E
A)Chứng Minh ΔABD = ΔEBD , từ đó suy ra AD =ED
B) gọi K là giao điểm của tia BA và tia ED . chứng Minh ΔKDC cân
Bài 3
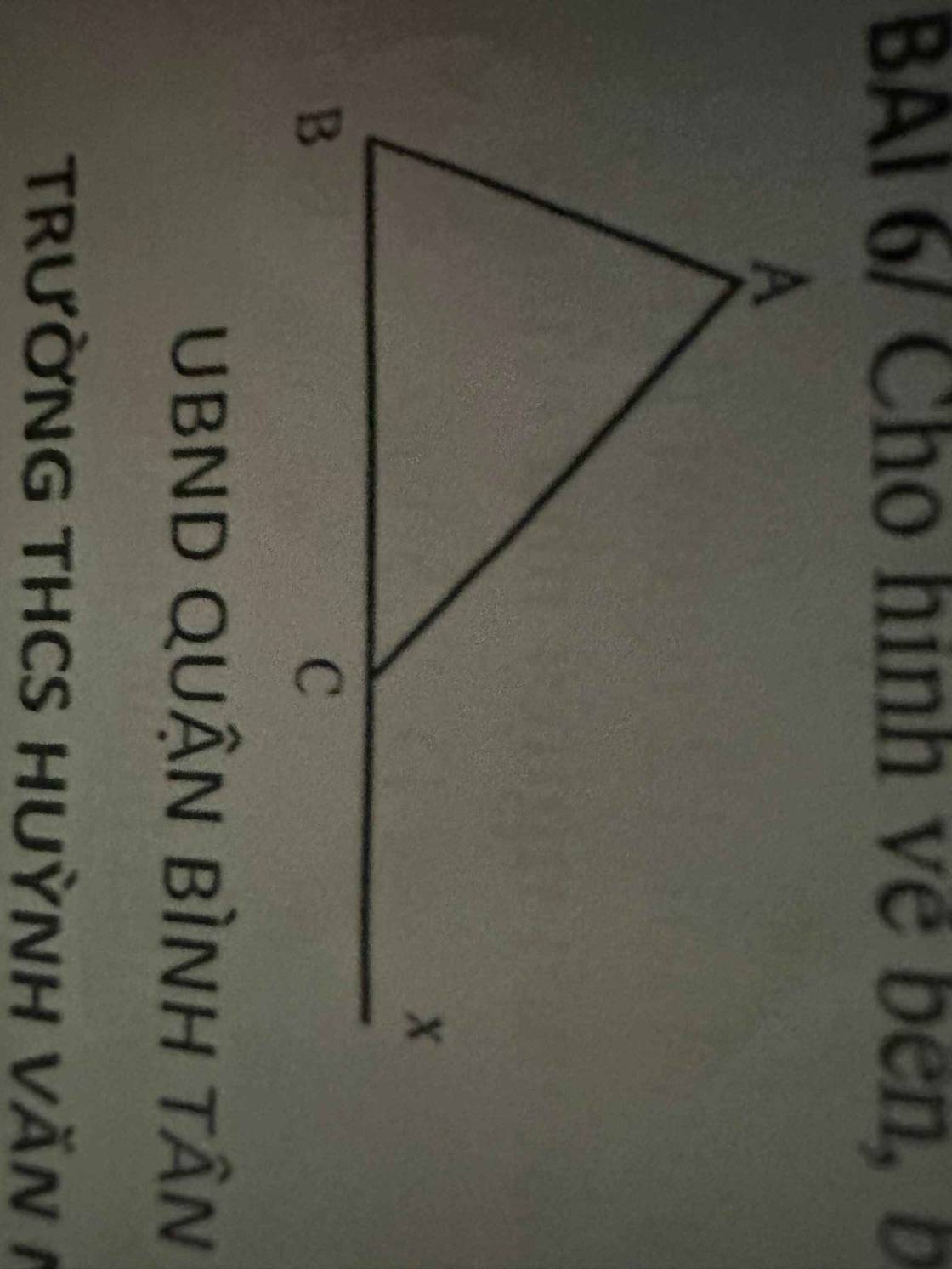
cho hình vẽ bên biết A =52 và ACX =120 tính số đo góc ABC ?
Cho tam giác ABC có ba góc nhọn và AB < AC. Vẽ AH vuông góc với BC tại H. Tia phân giác của góc C cắt AH tại M. Trên cạnh AC lấy điểm K sao cho CK = CH.
a) Chứng minh: MH = MK.
b) Chứng minh: CM ⊥ HK
c) Đường thẳng vuông góc với AC tại C cắt đường thẳng AH tại N.
Chứng minh: NMC = NCM
Cho tam giác abc vuông tại A,AB=9cm,AC=12cm. Gọi BD là tia phân giác của góc ABC (D thuộc AC).Qua D kẻ DE vuông góc BC (E thuộc BC)
a)Tính độ dài BC
b)Chứng minh tam giác ABC=Tam giác EBD
c)Chứng minh AD<DC
d) gọi I là giao điểm của DE và AB.Chứng minh BIC cân
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC,E là điểm thuộc đoạn thẳng BM ( E khác B và M). Kẻ BH,CK vuông góc với AE(H,K thuộc đoạn thẳng AE).
a) Chứng minh rằng BH = AK
b) Tính số đo góc MHK?
cho tam giác abc, AB=AC(góc A <90 độ) kẻ bh vuông góc với ac (H thuộc AC) CK vuông góc với AB (K thuộc AB) gọi I là giao điểm cuả BH và CK
a, Chứng minh tam giác BHC = tam giác CKB
b, Chứng minh IB=IC và góc IBK = góc ICH
c, Chứng minh KH // BC
d, cho BC=5cm,CH=3cm. tính chu vi và diện tích của tam giác AHB.
Cho △ABC Vuông tại A lấy điểm E trên cạch BC sao cho BE=BA .Đường thẳng vuông góc với BC tại E cát AC tại I
a)Chứng minh △ABI=△EBI
b)Gọi F là giao điểm của BA và EI.Chứng minh △iFC cân
c)CHứng Minh rằng BI⊥CF
d)Gọi D là trung điểm của AC và H là giao điểm của AE với BI .Kẻ CH cắt ED tại G .Tìm x biết EG=3x -4 và GD=x
Tam giác MNP cân tại M E là trung điểm NP a chứng minh tam giác mne bằng tam giác mpe B kẻ EH vuông góc MN e k vuông góc MP chứng minh eh = EK C Chứng minh ME vuông góc HK
choΔabc cân tại a trên tia đối của bc và cb lấy theo thứ tự 2 điểm d và e sao cho bd=ce
A, chứng minh Δade cân
B, gọi m là trung điểm của bc. chưng minh am là tia phân giác của góc dae
C, từ b và c kẻ bh và ck theo thứ tự vuông góc với ad và ae chứng minh bh =ck
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt cạnh AC tại D. Trên BC lấy điểm E sao cho BA =BE
a). Chứng minh tam giác ABC = tam giác EDB
b). Chứng minh DE vuông góc với BC
c). Trên tia đối của tia AB, lấy điểm M sao cho AM = EC. Chứng minh MD = CD
