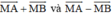a.
\(\left|\overrightarrow{BD}-\overrightarrow{BC}\right|=\left|\overrightarrow{BD}+\overrightarrow{CB}\right|=\left|\overrightarrow{CD}\right|=CD=a\)
b.
Do O là tâm hình vuông \(\Rightarrow\) O đồng thời là trung điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\\\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\end{matrix}\right.\)
Do đó:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\)
\(=4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}+\overrightarrow{OD}=4\overrightarrow{MO}+\overrightarrow{0}+\overrightarrow{0}=4\overrightarrow{MO}\)
c. Đề bài câu này thật kì quặc, đề cho cạnh hình vuông bằng a nhưng lại yêu cầu tìm quỹ tích có tổng độ dài bằng 1 đơn vị.
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=1\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=1\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=1\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=1\)
\(\Leftrightarrow3MG=1\)
\(\Leftrightarrow MG=\dfrac{1}{3}\)
Tập hợp M là đường tròn tâm G bán kính \(\dfrac{1}{3}\)