Bài 3:
$A=(x-5)(2x+3)-2x(x-3)+x+7$
$=2x^2+3x-10x-15-(2x^2-6x)+x+7$
$=2x^2-7x-15-2x^2+6x+x+7$
$=(2x^2-2x^2)+(6x+x-7x)+(7-15)=0+0-8=-8$ không phụ thuộc vào giá trị của biến.
$B=2x^2(x^2-3x)-6x+5+3x(2x^2+2)-2-2x^4$
$=2x^4-6x^3-6x+5+6x^3+6x-2-2x^4$
$=(2x^4-2x^4)+(-6x^3+6x^3)+(-6x+6x)+(5-2)$
$=0+0+0+3=3$ không phụ thuộc vào giá trị của biến.
Bài 4.
a. $36x^2-49=0$
$\Leftrightarrow (6x)^2-7^2=0$
$\Leftrightarrow (6x-7)(6x+7)=0$
$\Leftrightarrow 6x-7=0$ hoặc $6x+7=0$
$\Leftrightarrow x=\pm \frac{7}{6}$
b.
$(x-1)(x+2)=x+2$
$\Leftrightarrow (x-1)(x+2)-(x+2)=0$
$\Leftrightarrow (x+2)(x-1-1)=0$
$\Leftrightarrow (x+2)(x-2)=0$
$\Leftrightarrow x+2=0$ hoặc $x-2=0$
$\Leftrightarrow x=\pm 2$
c.
$x^2(x+1)+2x(x+1)=0$
$\Leftrightarrow (x+1)(x^2+2x)=0$
$\Leftrightarrow (x+1)x(x+2)=0$
$\Leftrightarrow x+1=0$ hoặc $x=0$ hoặc $x+2=0$
$\Leftrightarrow x=-1$ hoặc $x=0$ hoặc $x=-2$
c.
$x(2x-3)-2(3-2x)=0$
$\Leftrightarrow x(2x-3)+2(2x-3)=0$
$\Leftrightarrow (2x-3)(x+2)=0$
$\Leftrightarrow 2x-3=0$ hoặc $x+2=0$
$\Leftrightarrow x=\frac{3}{2}$ hoặc $x=-2$
e.
$2x^3(2x-3)-x^2(4x^2-6x+2)=0$
$\Leftrightarrow 2x^3(2x-3)-2x^2(2x^2-3x+1)=0$
$\Leftrightarrow 2x^2[x(2x-3)-(2x^2-3x+1)]=0$
$\Leftrightarrow 2x^2(-1)=0$
$\Leftrightarrow x^2=0\Leftrightarrow x=0$
f.
$(x-2)^2-(x+3)^2=5+4(x+1)$
$\Leftrightarrow (x-2-x-3)(x-2+x+3)=4x+9$
$\Leftrightarrow -5(2x+1)=4x+9$
$\Leftrightarrow -10x-5=4x+9$
$\Leftrightarrow -14x=14\Leftrightarrow x=-1$












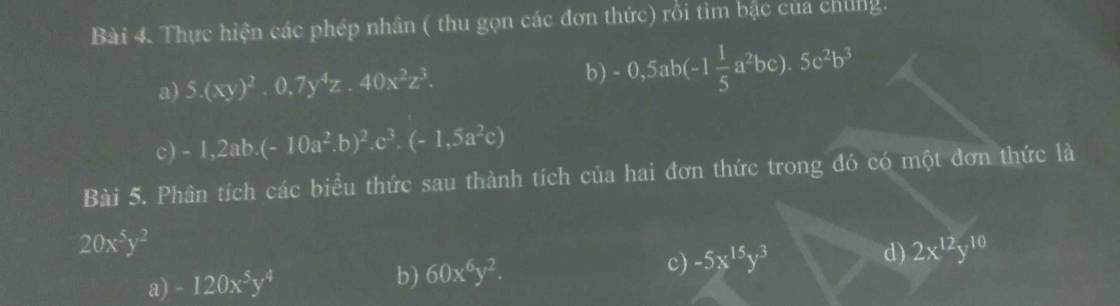





 bài 2 câu 1,2,3,5,9
bài 2 câu 1,2,3,5,9