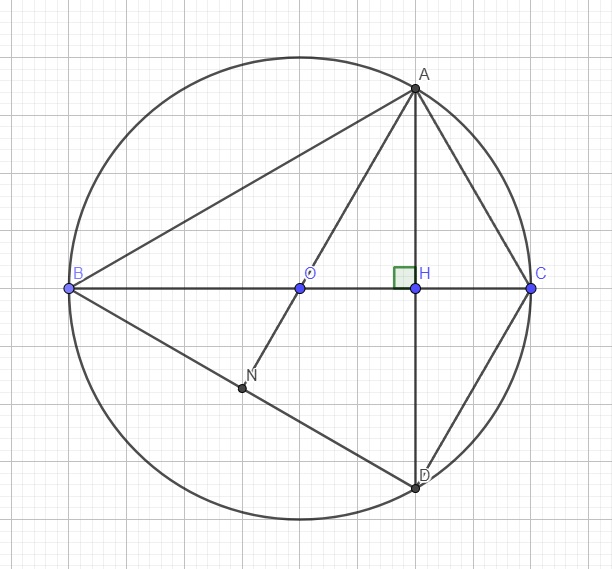
a: ΔOAD cân tại O
mà OH là đường cao
nên H là trung điểm của AD
Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
b: H là trung điểm của OC
=>\(HO=\dfrac{OC}{2}=2\left(cm\right)\)
ΔAHO vuông tại H
=>\(HA^2+HO^2=AO^2\)
=>\(HA^2=4^2-2^2=12\)
=>\(HA=2\sqrt{3}\left(cm\right)\)
=>\(AD=2\sqrt{3}\cdot2=4\sqrt{3}\left(cm\right)\)
BH=BO+OH=4+2=6(cm)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét ΔBAC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BA=\sqrt{6\cdot8}=4\sqrt{3}\left(cm\right)\)
=>AB=AD
=>AB=AD=BD
=>ΔBAD đều
Ta có: AB=AD
=>A nằm trên đường trung trực của BD(1)
ta có: OB=OD
=>O nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AO là đường trung trực của BD
=>AO\(\perp\)BD tại N
Xét tứ giác AHNB có \(\widehat{AHB}=\widehat{ANB}=90^0\)
nên AHNB là tứ giác nội tiếp
c: ΔBAC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+\left(4\sqrt{3}\right)^2=8^2\)
=>\(AC^2=64-48=16=4^2\)
=>AC=4(cm)
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>\(DB^2+DC^2=BC^2\)
=>\(DC^2=64-48=16\)
=>DC=4(cm)
\(S_{BACD}=S_{BAC}+S_{BDC}\)
\(=\dfrac{1}{2}\cdot BA\cdot AC+\dfrac{1}{2}\cdot BD\cdot DC\)
\(=\dfrac{1}{2}\cdot4\cdot4\sqrt{3}+\dfrac{1}{2}\cdot4\cdot4\sqrt{3}=4\cdot4\sqrt{3}=16\sqrt{3}\left(cm^2\right)\)
Diện tích (O) là:
\(S_{\left(O\right)}=4^2\Omega=16\Omega\left(cm^2\right)\)
Diện tích phần (O) nằm ngoài ABDC là: \(16\Omega-16\sqrt{3}\left(cm^2\right)\)
a.
DO BC vuông góc AD tại H, mà BC là đường kính \(\Rightarrow H\) là trung điểm AD
Hay \(AH=DH\)
\(\Rightarrow BC\) là đường trung trực của AD
\(\Rightarrow BA=BD\)
\(\Rightarrow\Delta ABD\) cân tại B
b.
Do H là trung điểm OC \(\Rightarrow OH=\dfrac{1}{2}OC=\dfrac{1}{4}BC=2\left(cm\right)\)
\(OA=OC=R=\dfrac{1}{2}BC=4\left(cm\right)\)
Áp dụng Pitago trong tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=2\sqrt{3}\) (cm)
Pitago trong tam giác vuông ABH:
\(AB=\sqrt{BH^2+AH^2}=\sqrt{\left(OB+OH\right)^2+AH^2}=4\sqrt{3}\) (cm)
\(AD=2AH=2.2\sqrt{3}=4\sqrt{3}\left(cm\right)\)
\(\Rightarrow AB=AD\Rightarrow\Delta ABD\) đều (1)
Lại có H là trung điểm AD \(\Rightarrow\) BH là trung tuyến của tam giác ABD, mà \(\dfrac{BO}{BH}=\dfrac{4}{4+2}=\dfrac{2}{3}\)
\(\Rightarrow\) O là trọng tâm tam giác ABD
\(\Rightarrow AO\) là 1 trung tuyến của tam giác ABD (2)
(1);(2) \(\Rightarrow AN\) là trung tuyến kiêm đường cao \(\Rightarrow AN\perp BD\)
\(\Rightarrow N\) và H cùng nhìn AB dưới 1 góc vuông nên ABHN nội tiếp
c.
\(S_{\left(O\right)}=\pi R^2=\pi.4^2=16\pi\left(cm^2\right)\)
\(S_{ABCD}=\dfrac{1}{2}.AD.BC=\dfrac{1}{2}.4\sqrt{3}.8=16\sqrt{3}\left(cm^2\right)\)
\(\Rightarrow\) Phần diện tích (O) nằm ngoài ABCD là:
\(S=S_{\left(O\right)}-S_{ABCD}=16\pi-16\sqrt{3}\) \(\left(cm^2\right)\)