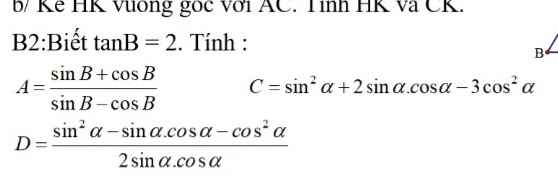1) G/s 2 điểm đó là \(A\left(-1;y_1\right)\) và \(B\left(2;y_2\right)\)
\(\Rightarrow\hept{\begin{cases}y_1=-\left(-1\right)^2=-1\\y_2=-2^2=-4\end{cases}}\)
\(\Rightarrow A\left(-1;-1\right)\) và \(B\left(2;-4\right)\)
PT đường thẳng đó công thức là \(y=ax+b\Rightarrow\hept{\begin{cases}-a+b=-1\\2a+b=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-1\\b=-2\end{cases}}\)
Vậy PT đường thẳng đó là \(y=-x-2\)
2)
a) Với m = -1 : \(x^2-2\cdot\left(-1-1\right)x--1-3=0\)
\(\Leftrightarrow x^2+4x-2=0\)
\(\Leftrightarrow\left(x+2\right)^2=6\Rightarrow x=-2\pm\sqrt{6}\)
b) \(\Delta^'=\left[-\left(m-1\right)\right]^2-1\cdot\left(-m-3\right)\)
\(=m^2-2m+1+m+3=m^2-m+4>0\left(\forall m\right)\)
=> PT luôn có 2 nghiệm phân biệt với mọi m
Theo hệ thức viet: \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1x_2=-m-3\end{cases}}\)
Ta có: \(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)=14\)
\(\Leftrightarrow4m^2-8m+4+2m+6-14=0\)
\(\Leftrightarrow4m^2-6m-4=0\)
\(\Leftrightarrow2m^2-3m-2=0\)
\(\Leftrightarrow m\left(2m+1\right)-2\left(2m+1\right)=0\)
\(\Leftrightarrow\left(m-2\right)\left(2m+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}m=2\\m=-\frac{1}{2}\end{cases}}\left(tm\right)\)
Vậy \(m\in\left\{2;-\frac{1}{2}\right\}\)
Bài 6.2
a, Thay m = -1 vào phương trình trên ta được
\(x^2+4x-2=0\)
\(\Delta=16-4\left(-2\right)=24>0\)
Vậy phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-4-\sqrt{24}}{2}=-2-\sqrt{6};x_2=\frac{-4+\sqrt{24}}{2}=-2+\sqrt{6}\)
Theo Vi et : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m-2\\x_1x_2=\frac{c}{a}=-m-3\end{cases}}\)
Lại có : \(\left(x_1+x_2\right)^2=\left(2m-2\right)^2=4m^2-8m+4\)
\(\Rightarrow x_1^2+x_2^2=4m^2-8m+4-2\left(-m-3\right)=4m^2-6m+10\)
\(x_1^2+x_2^2=14\Rightarrow4m^2-6m+10=14\)
\(\Leftrightarrow4m^2-6m-4=0\Leftrightarrow2m^2-3m-2=0\)
\(\Leftrightarrow\left(m-2\right)\left(2m+1\right)=0\Leftrightarrow m=-\frac{1}{2};m=2\)
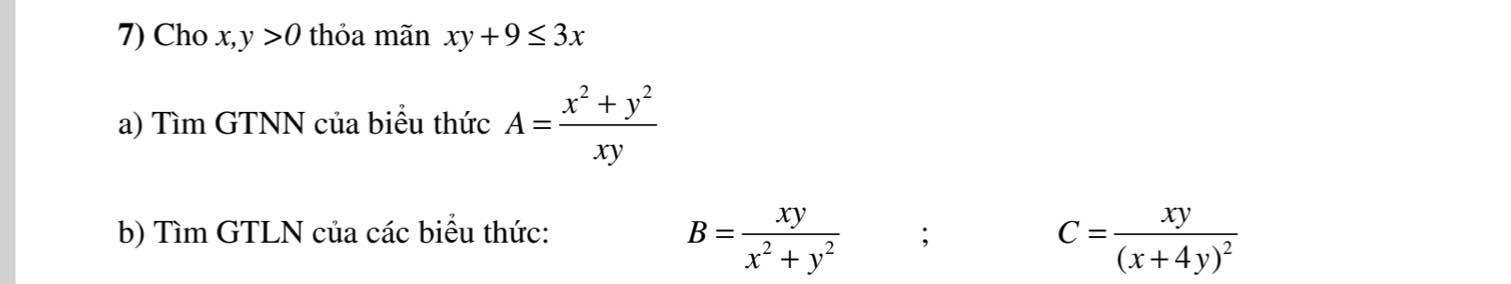mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
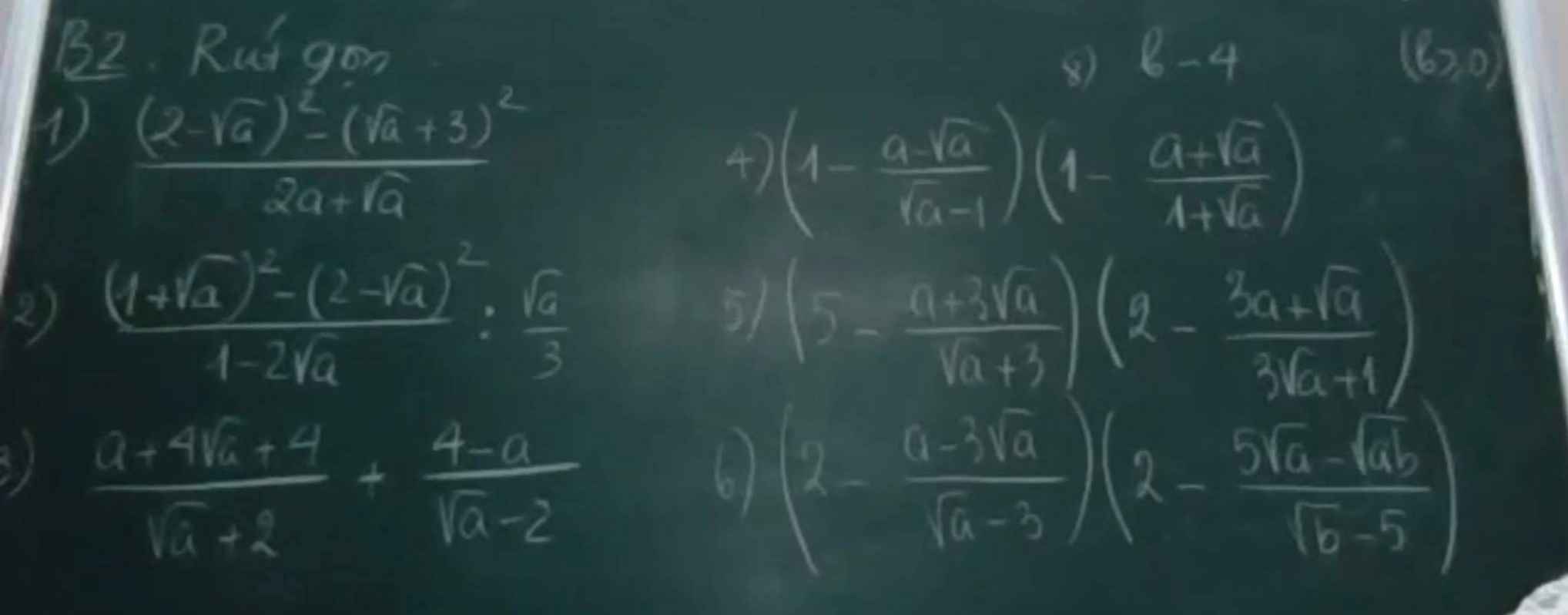
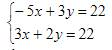ai giúp em bài này với ạ 🥺 :)
