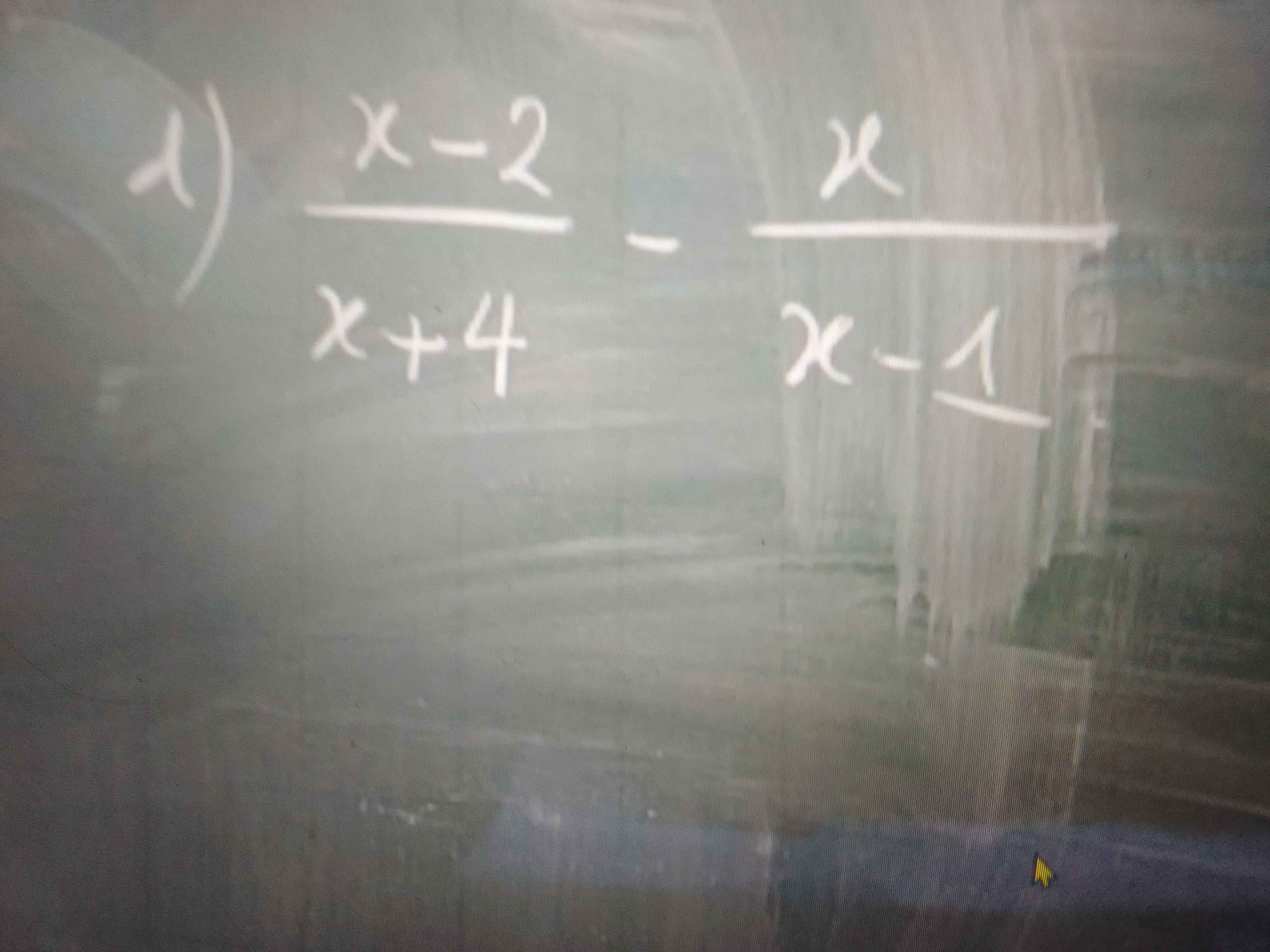\(d,=\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x+4\right)\left(x-1\right)}-\dfrac{x\left(x+4\right)}{\left(x+4\right)\left(x-1\right)}=\dfrac{x^2-x-2x+2-x^2-4x}{\left(x+4\right)\left(x-1\right)}=\dfrac{7x-2}{x^2+3x-4}\)
\(e,=\dfrac{\left(5x-1\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}+\dfrac{\left(3x-1\right)\left(x-2\right)}{\left(x-2\right)\left(x+3\right)}=\dfrac{5x^2+15x-x-3+3x^2-6x-x+2}{\left(x-2\right)\left(x+3\right)}=\dfrac{8x^2+7x-1}{x^2+x-6}\)
Đúng 1
Bình luận (0)
