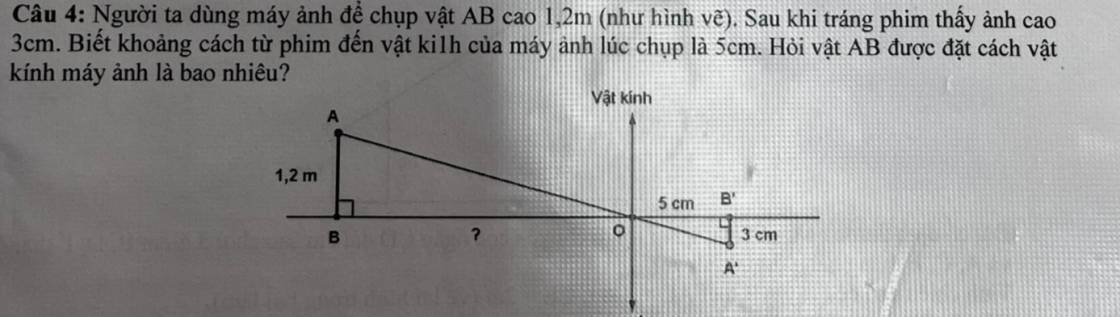
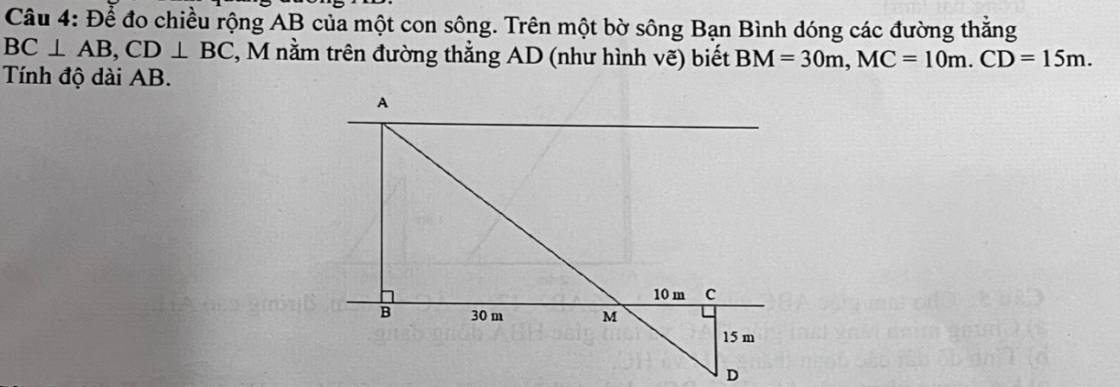
cho tam giác abc vuông tại a có ab=12cm ac=16cm đường cao ah.
a) chứng minh tam giác hba đồng dạng tam giác abc
b) tính bc, ah, bh
c) vẽ đường phân giác ad của tam giác abc. tính bd, cd
d) trên ah lấy điểm k sao cho ak = 3.6cm. Từ k kẻ đường thẳng song song với bc cắt ab và ac lần lượt tại m và n. tính diện tích bmnc
giúp mik zới ạ, mik đang cần gấp ak