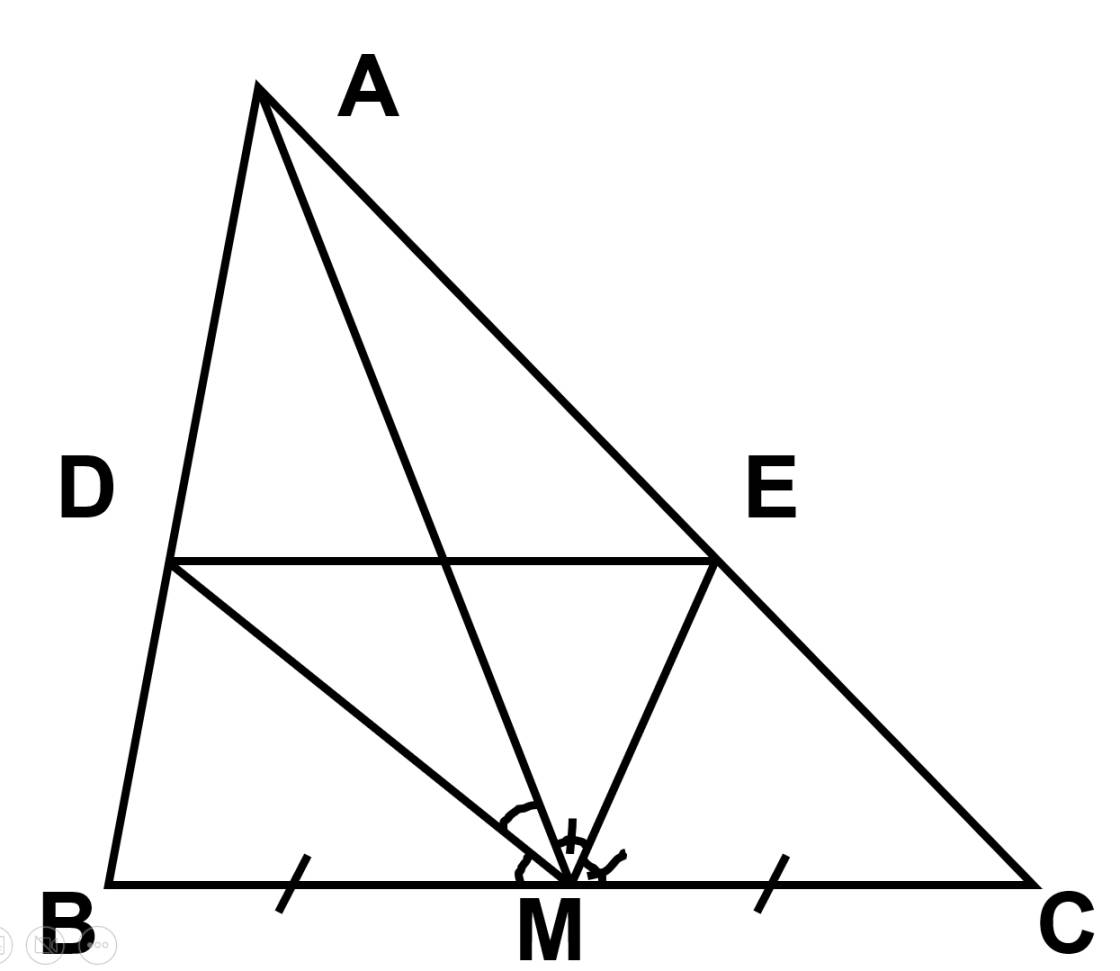
Cho Δ ABC, trung tuyến AM, đường phân giác của AMB cắt AB ở D, đường phân giác của AMC cắt AC ở E. Chứng minh rằng AD.ACC= AE.AB
Bài 3: Tính chất đường phân giác của tam giác
Xét ΔMAB có MD là phân giác
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)
=>\(\dfrac{AD}{DB}=\dfrac{AM}{MC}\left(1\right)\)
Xét ΔMAC có ME là phân giác
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
Xét ΔABC có DE//BC
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
Đúng 3
Bình luận (0)
Mình đang cần gấp ai giúp mình với!
Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm. Có 2 đường phân giác AD, BE cắt nhau tại I.
a, Tính độ dài AE, EC
b, Khoảng cách từ I đến đường thẳng AC
c, Độ dài phân giác AD ( làm tròn tới hàng phần trăm)
d, Diện tích tam giác DEI
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{AE}{AB}=\dfrac{CE}{CB}\)
=>\(\dfrac{AE}{5}=\dfrac{CE}{13}\)
mà AE+CE=AC=12
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{5}=\dfrac{CE}{13}=\dfrac{AE+CE}{5+13}=\dfrac{12}{18}=\dfrac{2}{3}\)
=>\(AE=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right);CE=13\cdot\dfrac{2}{3}=\dfrac{26}{3}\left(cm\right)\)
b: Kẻ IH\(\perp\)AC
=>IH là khoảng cách từ I xuống AC
IH\(\perp\)AC
AB\(\perp\)AC
Do đó: IH//AB
Xét ΔAEB có AI là phân giác
nên \(\dfrac{EI}{IB}=\dfrac{AE}{AB}=\dfrac{10}{3}:5=\dfrac{2}{3}\)
=>\(\dfrac{EI}{EB}=\dfrac{2}{5}\)
Xét ΔEAB có HI//AB
nên \(\dfrac{HI}{AB}=\dfrac{EI}{EB}\)
=>\(\dfrac{HI}{5}=\dfrac{2}{5}\)
=>HI=2(cm)
c: Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos45\)
=>\(AD=\dfrac{2\cdot5\cdot12}{5+12}\cdot\dfrac{\sqrt{2}}{2}\simeq4,99\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có đường cao AH. Phân giác trong của góc B cắt AH tại I. Biết AB = 10cm, AI/AH = 4/5. Chu vi tam giác ABC
\(\dfrac{AI}{AH}=\dfrac{4}{5}\)
=>\(AI=\dfrac{4}{5}AH\)
Ta có: AI+HI=AH
=>\(HI=AH-AI=AH-\dfrac{4}{5}AH=\dfrac{1}{5}AH\)
\(\dfrac{AI}{IH}=\dfrac{\dfrac{4}{5}AH}{\dfrac{1}{5}AH}=\dfrac{4}{5}:\dfrac{1}{5}=4\)
Xét ΔBAH có BI là phân giác
nên \(\dfrac{BA}{BH}=\dfrac{AI}{IH}\)
=>\(\dfrac{10}{BH}=4\)
=>BH=10/4=2,5(cm)
ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=5\left(cm\right)\)
Chu vi tam giác ABC là:
10+10+5=25(cm)
Đúng 1
Bình luận (1)
1. Cho tam giác ABC cân tại A. Đường phân giác góc B cắt AC tại M, đường phân giác góc C cắt AB tại N. Cm MN // BC.
2. Cho hình thoi ABCD. Trên cạnh BC, BA lần lượt lấy điểm E và F sao cho BF/BE=2/3. Đoạn thẳng FE cắt đoạn thẳng BD tại I.
a) Tính IE/IF.
b) Giả sử FE = 12cm. Tính độ dài IE và IF.
( Mình đang cần gấp mong các bạn giúp mình ạ.)
1. Ta có tam giác ABC cân tại A, do đó AB = AC.
Gọi I là giao điểm của đường phân giác góc B và đường phân giác góc C.
Ta cần chứng minh MN // BC.
Ta có:
∠BIM = ∠CIM (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIM = ∠CIM = ∠BIC/2 (do I nằm trên đường phân giác góc B và đường phân giác góc C)
∠BIC = ∠BAC (do tam giác ABC cân tại A)
∠BIC = ∠BAC = ∠BCA (do tam giác ABC cân tại A)
Do đó, ta có ∠BIM = ∠CIM = ∠BCA.
Từ đó, ta có MN // BC (do ∠MNI = ∠BCA và ∠MIN = ∠BAC).
Vậy ta đã chứng minh MN // BC.
2. a) Ta có BF/BE = 2/3.
Gọi x là độ dài của BE.
Do BF/BE = 2/3, ta có BF = (2/3)x.
Gọi y là độ dài của FE.
Do FE = 12cm, ta có y = 12cm.
Gọi z là độ dài của IF.
Do I là giao điểm của FE và BD, ta có IF/FE = BD/BE.
Do đó, IF/12 = BD/x.
Ta có BD = BC + CD = BC + BA = BC + BE.
Do đó, IF/12 = (BC + BE)/x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do đó, BC = BF + FC = (2/3)x + (1/3)x = x.
Vậy, IF/12 = (x + x)/x = 2.
Từ đó, ta có IF = 2 * 12 = 24cm.
Do đó, IE/IF = BE/FE = x/12.
Vậy, IE/IF = x/12.
b) Giả sử FE = 12cm.
Từ phần a), ta đã tính được IF = 24cm.
Do đó, IE/IF = x/12.
Ta cần tính x.
Ta có BF/BE = 2/3, nên BF = (2/3)x.
Do BF = (2/3)x và BC = x, ta có BC = BF + FC.
Do đó, x = (2/3)x + FC.
Từ đó, FC = (1/3)x.
Vậy, BC = BF + FC = (2/3)x + (1/3)x = x.
Do đó, BC = x = 12cm.
Vậy, độ dài của IE và IF lần lượt là 12cm và 24cm.
Đúng 0
Bình luận (2)
1: Xét ΔABC có BM là phân giác
nên \(\dfrac{AM}{MC}=\dfrac{AB}{BC}\)
=>\(\dfrac{AM}{MC}=\dfrac{AC}{BC}\left(1\right)\)
Xét ΔCAB có CN là phân giác
nên \(\dfrac{AN}{NB}=\dfrac{AC}{BC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AM}{MC}=\dfrac{AN}{NB}\)
Xét ΔABC có \(\dfrac{AM}{MC}=\dfrac{AN}{NB}\)
nên MN//BC
Đúng 0
Bình luận (0)
 làm theo tc đường phân giác chi tiết
làm theo tc đường phân giác chi tiết
Chi tiết vẽ hình
a: Xét ΔIAB có IE là phân giác
nên \(\dfrac{AE}{EB}=\dfrac{AI}{IB}\)
=>\(\dfrac{AE}{EB}=\dfrac{AI}{IC}\left(1\right)\)
Xét ΔIAC có IQ là phân giác
nên \(\dfrac{AQ}{QC}=\dfrac{IA}{IC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AQ}{QC}\)
Xét ΔABC có \(\dfrac{AE}{EB}=\dfrac{AQ}{QC}\)
nên EQ//BC
b: Xét ΔABI có EO//BI
nên \(\dfrac{EO}{BI}=\dfrac{AO}{AI}\left(3\right)\)
Xét ΔAIC có OQ//IC
nên \(\dfrac{OQ}{IC}=\dfrac{AO}{AI}\left(4\right)\)
Từ (3) và (4) suy ra \(\dfrac{EO}{BI}=\dfrac{OQ}{IC}\)
mà BI=IC
nên EO=OQ
=>O là trung điểm của EQ
Đúng 1
Bình luận (0)
tam giác ABC,đường cao AH,kẻ phân giác AD của góc HAC,phân giác HE của góc AHC
CM:DE//AH
cho tam giác ABC đều có cạnh là 7
a, tính độ dài đường cao AH
b,từ H kẻ HM⊥AC
tính HM,AM,MC
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=7/2=3,5
\(AH=\sqrt{AB^2-HB^2}=\dfrac{7\sqrt{3}}{2}\)
b: Xét ΔAHC vuông tại H có HM là đường cao
nên HM*AC=AH*HC
=>HM*7=7/2*căn 3*3,5=49/4*căn 3
=>HM=7/4*căn 3
AM=AH^2/AC=21/4
CM=7-21/4=7/4
Đúng 1
Bình luận (0)
Cho tam giác abc vuông tại a có ab 6 cm, bc 10 cm, bd là phân giác góc widehat{ABC} a)Tính da và dc b) Qua ac vẽ đường thẳng vuông góc với bd tại m cắt ab tại e. Chứng minh dfrac{em}{eb} dfrac{ea}{ec}
Đọc tiếp
Cho tam giác abc vuông tại a có ab= 6 cm, bc= 10 cm, bd là phân giác góc \(\widehat{ABC}\) a)Tính da và dc
b) Qua ac vẽ đường thẳng vuông góc với bd tại m cắt ab tại e. Chứng minh \(\dfrac{em}{eb}\) = \(\dfrac{ea}{ec}\)
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/BC
=>DA/3=DC/5=(DA+DC)/(3+5)=16/8=2
=>DA=6cm; DC=10cm
b: AD/DC=AB/BC
AH/AC=AB/BC
=>AD/DC=AH/AC
=>AD*AC=DC*AH
Đúng 0
Bình luận (0)